Giải Toán 8 sách Kết nối Tri Thức, bài 10: Tứ giác
Giải Toán 8 sách Kết nối Tri Thức, bài 10: Tứ giác - Trang 49, 50, 51.
1. Tứ giác lồi
Câu hỏi trang 49: Cho bốn điểm E, F, G, H (Hình 3.3). Kể tên một tứ giác có các đỉnh là bốn điểm đã cho.
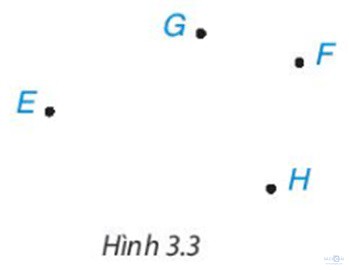
Giải:
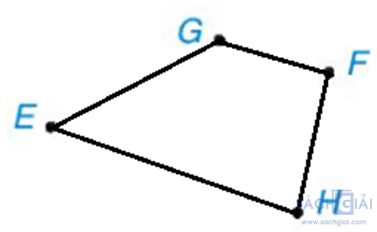
Nối EG, GF, FH, HE, ta được tứ giác EGFH như hình vẽ.
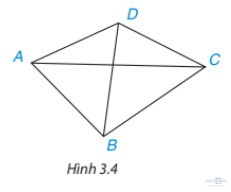
Luyện tập 1 trang 49: Quan sát tứ giác ABCD trong Hình 3.4.
Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại.
Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại.
Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.
Giải:
Đường chéo: BD
Cặp cạnh đối: Ad và BC
Cặp góc đối: B và C

Giải:
Nối EG, GF, FH, HE, ta được tứ giác EGFH như hình vẽ.

Luyện tập 1 trang 49: Quan sát tứ giác ABCD trong Hình 3.4.
Hai đỉnh không cùng thuộc một cạnh gọi là hai đỉnh đối nhau. Đoạn thẳng nối hai đỉnh đối nhau là một đường chéo, chẳng hạn AC là một đường chéo. Kể tên đường chéo còn lại.
Cặp cạnh AB, CD là cặp cạnh đối. Chỉ ra cặp cạnh đối còn lại.
Cặp góc A, C là cặp góc đối. Hãy kể tên cặp góc đối còn lại.

Giải:
Đường chéo: BD
Cặp cạnh đối: Ad và BC
Cặp góc đối: B và C
2. Tổng các góc của một tứ giác
Hoạt động trang 50: Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng 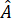 +
+ 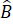 +
+ 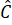 +
+ 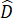 của tứ giác ABCD
của tứ giác ABCD
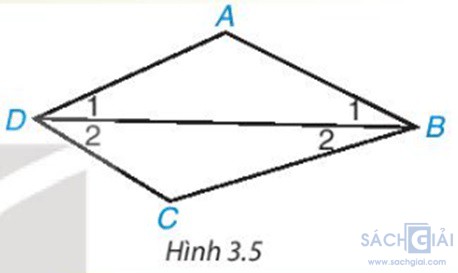
Giải:
Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:
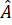 +
+ 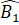 +
+ 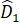 = 180o
= 180o
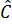 +
+ 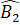 +
+ 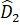 = 180o
= 180o
Khi đó, tứ giác ABCD có:
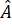 +
+ 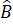 +
+ 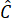 +
+ 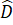 =
= 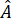 +
+ 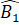 +
+ 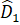 +
+ 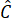 +
+ 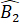 +
+ 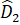 = 180o + 180o = 360o
= 180o + 180o = 360o
Vậy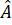 +
+ 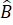 +
+ 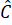 +
+ 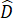 = 180o
= 180o
Luyện tập 2 trang 50: Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F
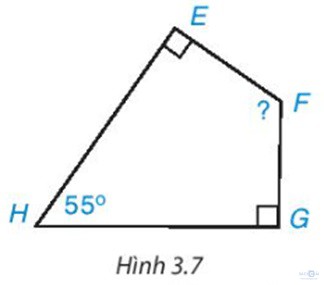
Giải:
Xét tứ giác EFGH có:
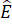 +
+ 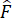 +
+ 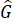 +
+ 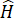 = 360o (định lí tổng các góc trong một tứ giác).
= 360o (định lí tổng các góc trong một tứ giác).
Hay 90° +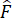 + 90o + 55o = 360o
+ 90o + 55o = 360o
Suy ra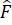 + 235o = 360o
+ 235o = 360o
Do đó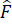 = 360o – 235o = 125o
= 360o – 235o = 125o
Vậy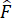 = 125o
= 125o
Vận dụng trang 50: Giải bài toán mở đầu.
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
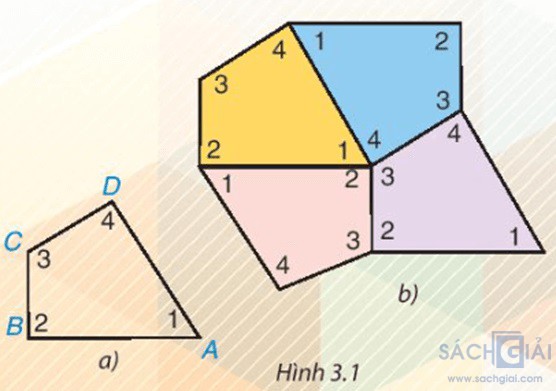
- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.
Giải:
- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó:
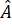 +
+ 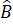 +
+ 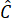 +
+ 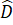 = 360°
= 360°

Giải:
Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:
Khi đó, tứ giác ABCD có:
Vậy
Luyện tập 2 trang 50: Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F

Giải:
Xét tứ giác EFGH có:
Hay 90° +
Suy ra
Do đó
Vậy
Vận dụng trang 50: Giải bài toán mở đầu.
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.

- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo của bốn góc đó.
Giải:
- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó:
3. Giải bài tập trang 51:
Bài 3.1: Tính góc chưa biết của các tứ giác trong Hình 3.8
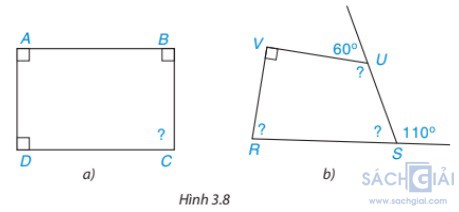
Giải:
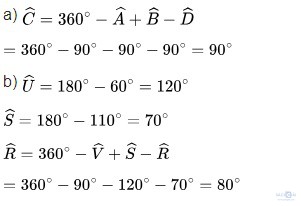
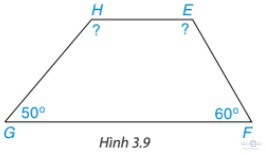
Bài 3.2: Tính góc chưa biết của tứ giác trong Hình 3.9. Biết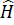 =
= 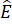 + 10o
+ 10o
Giải:
Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:
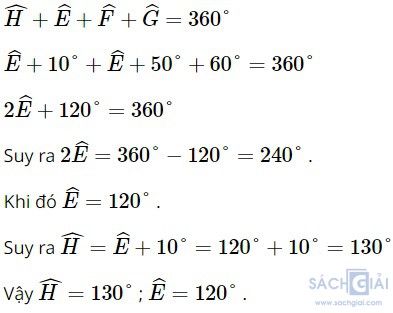
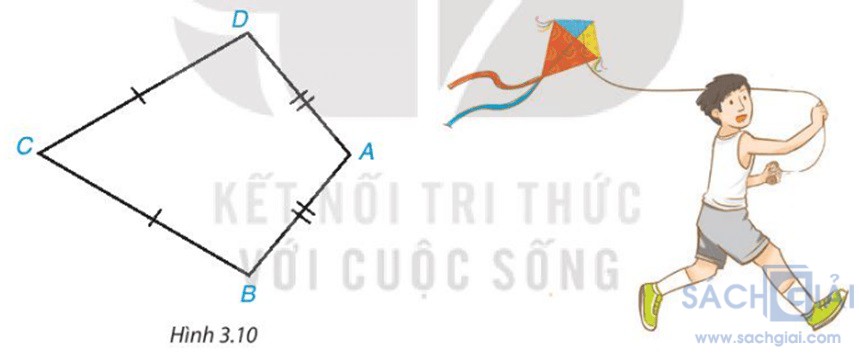
Bài 3.3: Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của đoạn BD
b) Tính các góc B, D biết rằng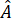 = 100o,
= 100o, 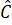 = 60o
= 60o
Giải:
a) Nối AC, BD (như hình vẽ).
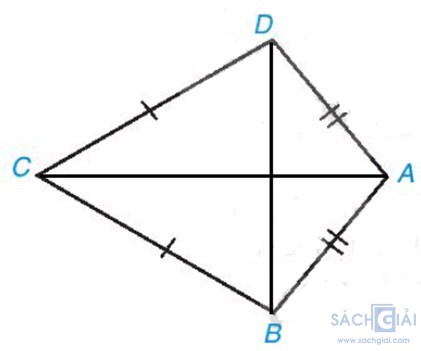
Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;
CB = CD hay hai điểm C cách đều hai đầu mút B và D;
Do đó, hai điểm A và C cách đều hai đầu mút B và D.
Vậy AC là đường trung trực của đoạn thẳng BD.
b) Gọi I là giao điểm của AC và BD.
Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.
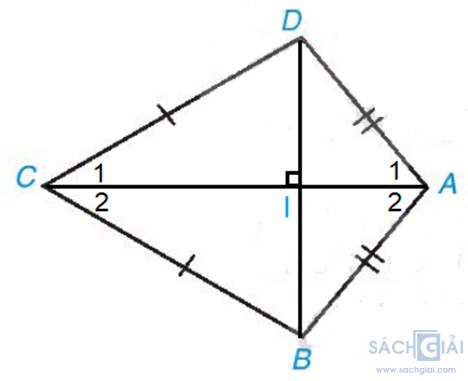
• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)
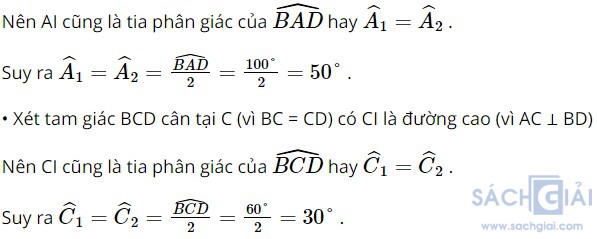
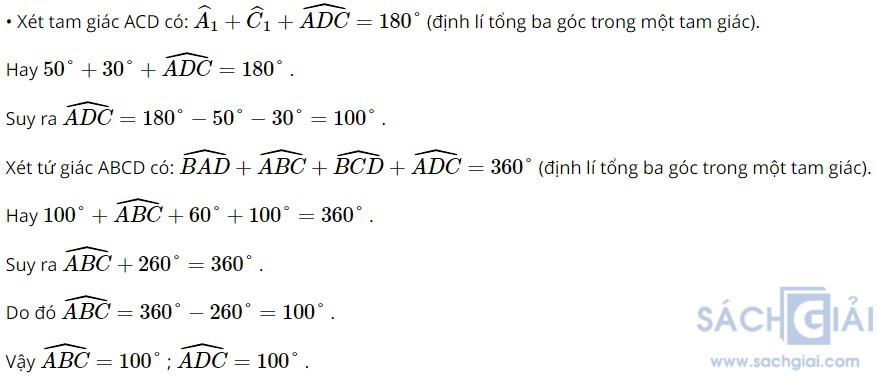

Giải:
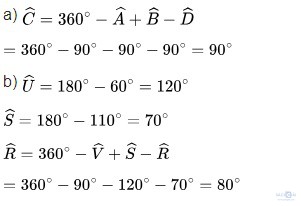
Bài 3.2: Tính góc chưa biết của tứ giác trong Hình 3.9. Biết

Giải:
Áp dụng định lí tổng bốn góc trong một tứ giác vào tứ giác HEFG, ta có:
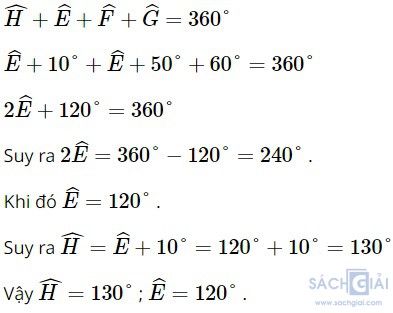
Bài 3.3: Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của đoạn BD
b) Tính các góc B, D biết rằng

Giải:
a) Nối AC, BD (như hình vẽ).

Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;
CB = CD hay hai điểm C cách đều hai đầu mút B và D;
Do đó, hai điểm A và C cách đều hai đầu mút B và D.
Vậy AC là đường trung trực của đoạn thẳng BD.
b) Gọi I là giao điểm của AC và BD.
Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.

• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)
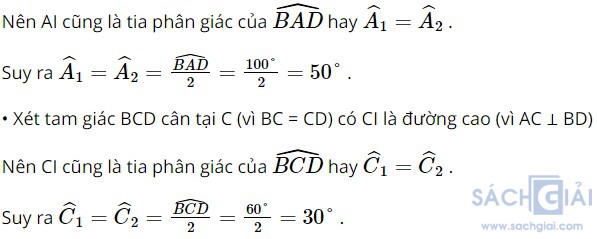
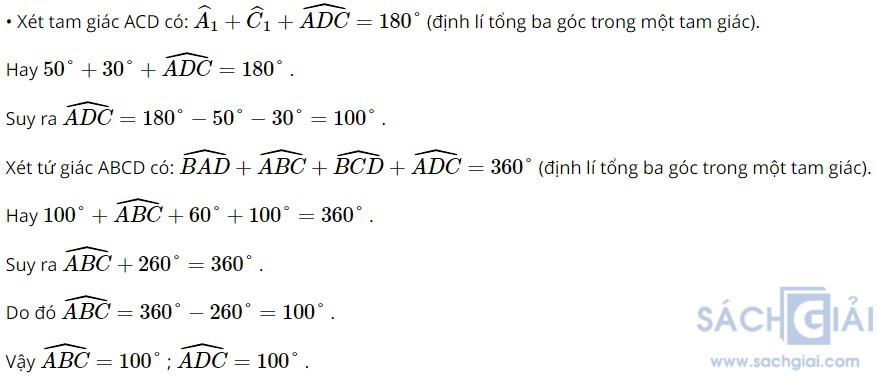
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025