Giải Toán 8 sách Kết nối Tri Thức, bài 11: Hình thang cân
Giải Toán 8 sách Kết nối Tri Thức, bài 11: Hình thang cân - Trang 53, 54, 55
1. Hình thang. Hình thang cân
Luyện tập 1 trang 53: Tính các góc của hình thang cân ABCD (AB // CD, biết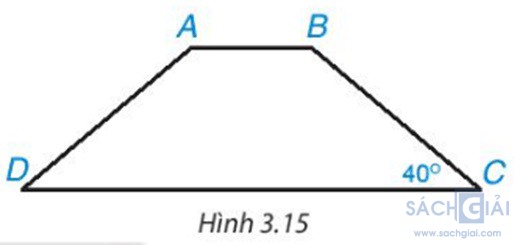
Giải:
Hình thang cân ABCD (AB // CD) nên ta có:
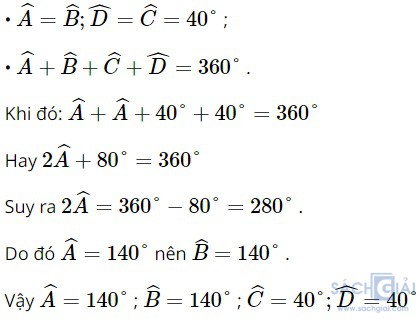
2. Tính chất của hình thang cân
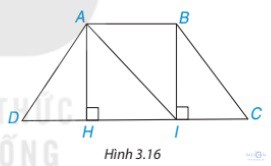
Hoạt động 1 trang 53: Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16).a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.
Giải:
a) Xét tam giác vuông AHI và IBA ta có:
AI chung
Suy ra, ∆ AHI = ∆ IBA (cạnh huyền - góc nhọn)
=> AH = BI
b) Xét tam giác AHD và BIC ta có:
AH = BI
Suy ra, ∆ AHD = ∆ BIC
=> AD = BC
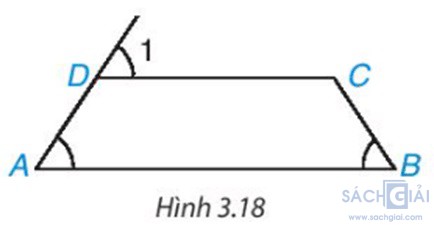
Luyện tập 2 trang 53: Cho tứ giác ABCD như Hình 3.18. Biết rằng A
Giải:
Ta có
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có
Do đó AD = BC (đpcm).
Hoạt động 2 trang 54: Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ ACD = ∆ BDC. Từ đó suy ra AC = BD.
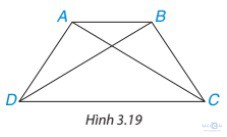
Giải:
Vì ABCD là hình thang cân (AB // CD) nên AD = BC;
Xét ∆ACD và ∆BDC có
AD = BC (chứng minh trên);
Cạnh CD chung.
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
Luyện tập 3 trang 54: Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
a) Tứ giác DECB là hình gì?
b) Chứng minh BE = CD.
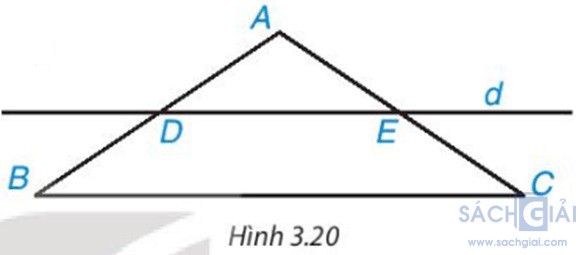
Giải:
a) Theo đề bài: d // BC nên DE // BC
Suy ra DECB là hình thang.
Vì tam giác ABC cân tại A nên
Hình thang DECB có
b) Hình thang cân DECB có BE và CD là hai đường chéo.
Do đó BE = CD (đpcm).
3. Giải bài tập trang 55
Bài 3.4: Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?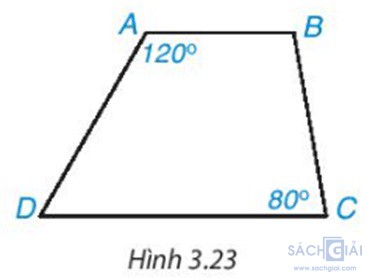
Giải:
Do ABCD là hình thang có AB // CD nên ta có:
Suy ra
Hình thang ABCD có
Cách 2:
Giả sử hình thang ABCD là hình thang cân. Khi đó
Suy ra
Khi đó, ABCD không phải là tứ giác, điều này mâu thuẫn với giả thiết ABCD là hình thang cân (hình thang cân cũng là tứ giác).
Do đó ABCD không phải là hình thang cân.
Bài tập 3.5: Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân
Giải:
Gọi O là giao điểm của AC và BD.
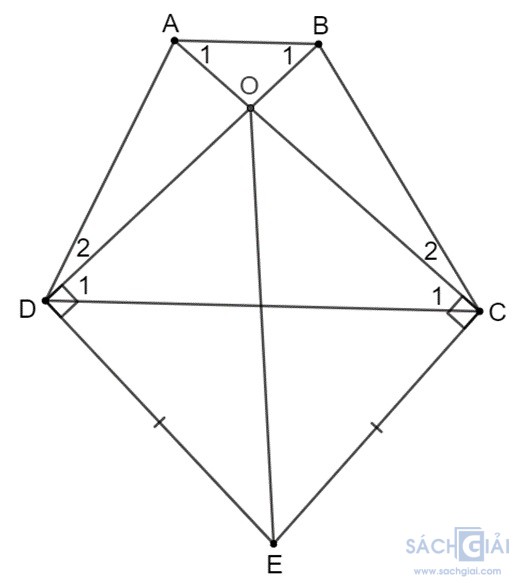
Xét ∆DOE và ∆COE có:
EC = ED (giả thiết);
Cạnh OE chung
Do đó ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).
Suy ra OC = OD (hai cạnh tương ứng) (1)
Do đó tam giác OCD cân tại O nên
Vì ABCD là hình thang nên AB // CD suy ra
Do đó
Suy ra tam giác OAB cân tại O nên OA = OB (2)
Ta có: AC = OA + OC và BD = OB + OD (3)
Từ (1), (2) và (3) suy ra AC = BD
Hình thang ABCD có AC = BD nên ABCD là hình thang cân.
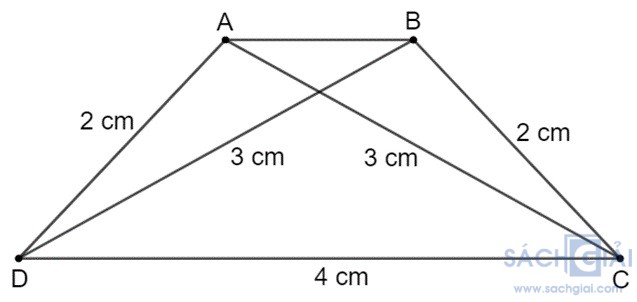
Bài 3.6: Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm
Giải:
Cách vẽ hình thang cân ABCD có đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm:
– Vẽ cạnh CD = 4 cm.
– Dùng compa vẽ hai đường tròn (D; 2 cm) và (C; 3 cm). Hai đường tròn này cắt nhau tại điểm A.
– Dùng compa vẽ hai đường tròn (D; 3 cm) và (C; 2 cm). Hai đường tròn này cắt nhau tại điểm B.
– Nối AB, AD, BC ta được hình thang cân ABCD (như hình vẽ).
Bài 3.7: Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB// CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED
Giải:
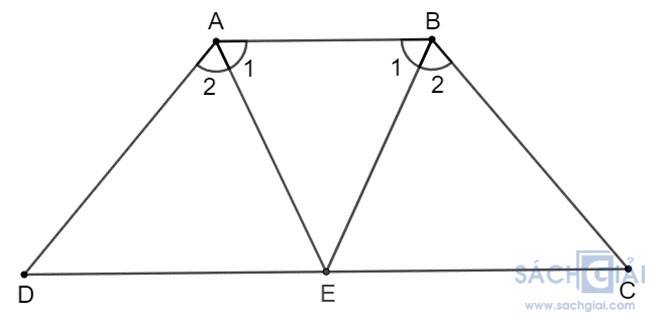
Vì ABCD là hình thang cân nên
Theo đề bài, ta có AE, BE lần lượt là tia phân giác của
Suy ra
Mà
Xét tam giác EAB cân tại E (vì A1
Xét ∆ADE và ∆BCE có:
EA = EB (chứng minh trên);
AD = BC (chứng minh trên)
Do đó ∆ADE = ∆BCE (c.g.c).
Suy ra EC = ED (hai cạnh tương ứng).
Bài 3.8: Hình thang cân ABCD (AB // CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB
Giải:
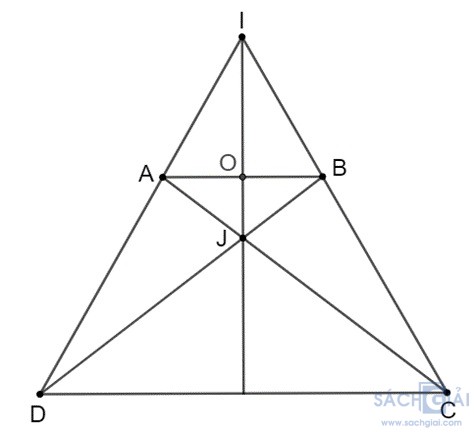
Vì ABCD là hình thang cân nên
Xét DICD cân tại I (vì
Suy ra IC – BC = ID – AD, hay IB = IA
Do đó I cách đều A và B nên I nằm trên đường trung trực của AB (1)
Xét ∆ABD và ∆BAC có:
AB là cạnh chung;
AD = BC (chứng minh trên).
Do đó ∆ABD = ∆BAC (c.g.c)
Suy ra
Tam giác JAB cân tại J (vì
Do đó J cách đều A và B nên J nằm trên đường trung trực của AB (2)
Từ (1) và (2) suy ra I, J cùng nằm trên đường thẳng IJ là đường trung trực của đoạn thẳng AB.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025