Giải Toán 8 sách Kết nối Tri Thức, bài: Luyện tập chung - Trang 56.
Giải Toán 8 sách Kết nối Tri Thức, bài: Luyện tập chung - Trang 56.
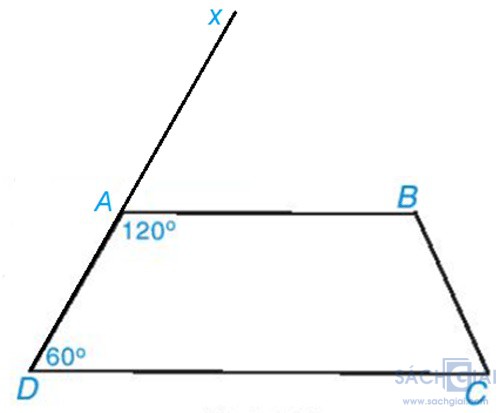
Bài 3.9. Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?
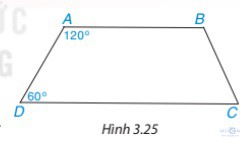
Giải:

Bài 3.10: Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết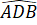 = 60o, tính số đo các góc của hình thang đó.
= 60o, tính số đo các góc của hình thang đó.
Giải:
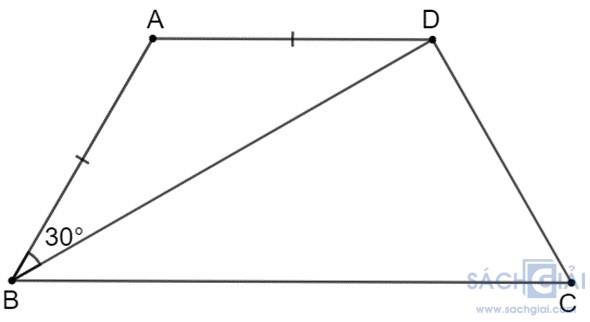
Xét tam giác ABD cân tại A (vì AB = AD), ta có:
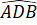 =
= 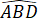 = 30o
= 30o
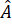 +
+ 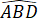 +
+ 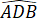 = 180o hay
= 180o hay 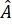 + 30o + 30o = 180o
+ 30o + 30o = 180o
Suy ra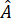 = 180o – 30o – 30o = 120o
= 180o – 30o – 30o = 120o
Vì AB // CD nên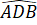 =
= 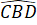 = 30o (hai góc so le trong).
= 30o (hai góc so le trong).
Do đó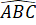 =
= 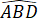 +
+ 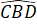 = 30o + 30o = 60o
= 30o + 30o = 60o
Vì tứ giác ABCD là hình thang cân nên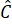 =
= 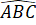 = 60o;
= 60o; 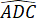 =
= 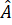 = 120o
= 120o
Vậy số đo các góc của hình thang cân ABCD là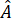 = 120o ;
= 120o ; 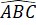 = 60o;
= 60o; 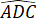 = 120o
= 120o
Bài 3.11: Tính số đo các góc của tứ giác ABCD trong Hình 3.26
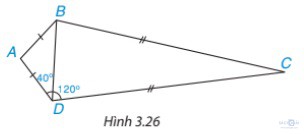
Giải:
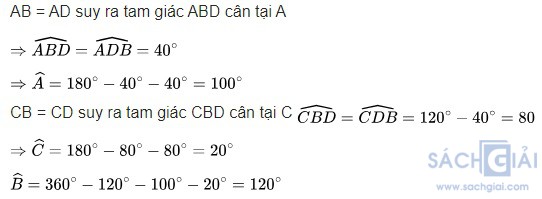
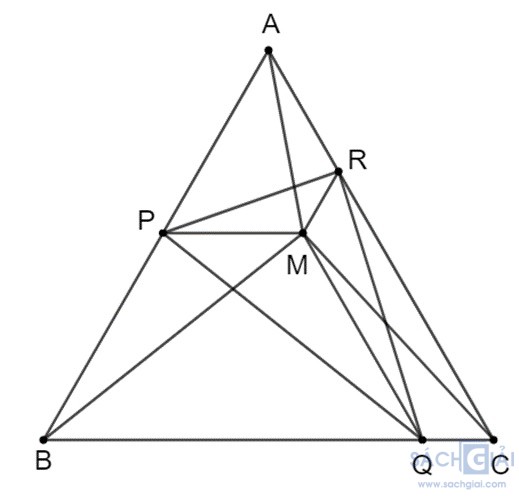
Bài 3.12: Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R
a) Chứng minh tứ giác APMR là hình thang cân
b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC
c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?
Giải:
a) Vì tam giác ABC đều nên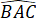 =
= 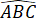 =
= 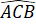 = 60o
= 60o
Vì PM // BC nên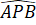 =
= 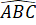 = 60o (đồng vị).
= 60o (đồng vị).
Suy ra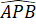 =
= 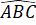 (cùng bằng 60°).
(cùng bằng 60°).
Tứ giác APMR là hình thang (vì MR // AP) có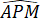 =
= 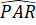
Do đó tứ giác APMR là hình thang cân.
b) Vì tứ giác APMR là hình thang cân nên AM = PR (1)
Chứng minh tương tự câu a, ta cũng có các tứ giác BPMQ và MQCR là hình thang cân.
Suy ra BM = PQ và MC = QR (2)
Từ (1)và (2) suy ra PR + PQ + QR = MA + MB + MC.
Mà PR + PQ + QR chính là chu vi của tam giác PQR.
Do đó chu vi tam giác PQR bằng tổng độ dài MA + MB + MC (đpcm).
c) Để tam giác PQR là tam giác đều thì PR = PQ = QR suy ra MA = MB = MC
Khi đó điểm M cách đều ba đỉnh A, B, C của tam giác ABC.
Do đó M là giao điểm của ba đường trung trực (đồng thời M cũng là giao điểm của ba đường trung tuyến, ba đường cao, đường phân giác).
Vậy khi M là giao điểm của ba đường trung trực thì tam giác PQR là tam giác đều.

Giải:


Bài 3.10: Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết
Giải:

Xét tam giác ABD cân tại A (vì AB = AD), ta có:
Suy ra
Vì AB // CD nên
Do đó
Vì tứ giác ABCD là hình thang cân nên
Vậy số đo các góc của hình thang cân ABCD là
Bài 3.11: Tính số đo các góc của tứ giác ABCD trong Hình 3.26

Giải:
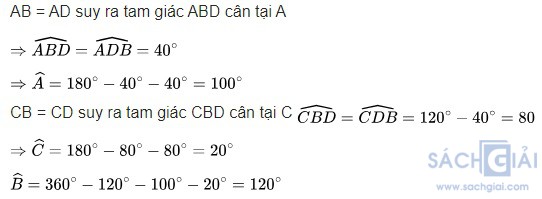
Bài 3.12: Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R
a) Chứng minh tứ giác APMR là hình thang cân
b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC
c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?
Giải:

a) Vì tam giác ABC đều nên
Vì PM // BC nên
Suy ra
Tứ giác APMR là hình thang (vì MR // AP) có
Do đó tứ giác APMR là hình thang cân.
b) Vì tứ giác APMR là hình thang cân nên AM = PR (1)
Chứng minh tương tự câu a, ta cũng có các tứ giác BPMQ và MQCR là hình thang cân.
Suy ra BM = PQ và MC = QR (2)
Từ (1)và (2) suy ra PR + PQ + QR = MA + MB + MC.
Mà PR + PQ + QR chính là chu vi của tam giác PQR.
Do đó chu vi tam giác PQR bằng tổng độ dài MA + MB + MC (đpcm).
c) Để tam giác PQR là tam giác đều thì PR = PQ = QR suy ra MA = MB = MC
Khi đó điểm M cách đều ba đỉnh A, B, C của tam giác ABC.
Do đó M là giao điểm của ba đường trung trực (đồng thời M cũng là giao điểm của ba đường trung tuyến, ba đường cao, đường phân giác).
Vậy khi M là giao điểm của ba đường trung trực thì tam giác PQR là tam giác đều.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025