Giải bài tập SGK Toán 6: Luyện tập chung trang 43 - Sách Kết nối tri thức với cuộc sống
Giải bài tập SGK Toán 6: Luyện tập chung trang 43 - Sách Kết nối tri thức với cuộc sống
Câu 2.25 - Trang 43: Từ các chữ số 5; 0; 1; 3, viết các số tự nhiên có ba chữ số khác nhau thỏa mãn:
a) Các số đó chia hết cho 5.
b) Các số đó chia hết cho 3.
Giải:
a) Số cần viết chia hết cho 5 nên nó có chữ số tận cùng là 0 hoặc 5. Vậy các số cần tìm là: 510; 150; 310; 130; 350; 530; 105; 305; 315; 135.
b) Số cần viết chia hết cho 3 nên tổng các chữ số của nó phải chia hết cho 3.
Từ các chữ số 5; 0; 1; 3, ta có hai cách nhóm thành bộ ba số có tổng chia hết cho 3:
5 + 0 + 1 = 6 chia hết cho 3.
5 + 1 + 3 = 9 chia hết cho 3.
Vậy các số cần tìm là: 501; 510; 105; 150; 513; 531; 135; 153; 351; 315.
Câu 2.26 - Trang 43:
Hãy phân tích các số A, B ra thừa số nguyên tố:
A = 42 . 63 ;
B = 92 . 152 .
Giải:

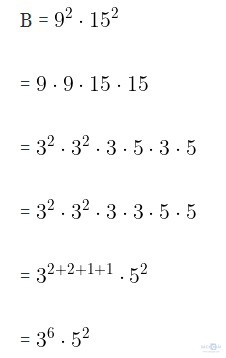
Bài tập 2.27 - Trang 43:
Tìm các số tự nhiên x không vượt quá 22 sao cho:
a) 100 – x chia hết cho 4.
b) 18 + 90 + x chia hết cho 9.
Giải:
a) Ta có: 100 – x chia hết cho 4. Mà 100 chia hết cho 4 nên x chia hết cho 4
Do đó x là bội của 4 và không vượt quá 22
Vậy x ∈ {0; 4; 8; 12; 16; 20}
b) Ta có: 18 + 90 + x chia hết cho 9. Mà 18 và 90 chia hết cho 9 nên x chia hết cho 9.
Do đó x là bội của 9 và không vượt quá 22
Vậy x ∈ {0; 9; 18}.
Bài tập 2.28 - Trang 43:
Lớp 6B có 40 học sinh. Để thực hiện dự án học tập nhỏ, cô giáo muốn chia lớp thành các nhóm có số người như nhau, mỗi nhóm nhiều hơn 3 người. Hỏi mỗi nhóm có thể có bao nhiêu người?
Giải:
Số người mỗi nhóm phải lớn hơn 3 và là ước của 40.
Mà Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}
Nên mỗi nhóm có thể có 4; 5; 8; 10; 20; hoặc 40 người.
Bài tập 2.29 - Trang 43:
Hai số nguyên tố được gọi là sinh đôi nếu chúng hơn kém nhau hai đơn vị. Ví dụ 17 và 19 là hai số nguyên tố sinh đôi. Em hãy liệt kê hết các cặp số nguyên tố sinh đôi nhỏ hơn 40.
Giải:
Các cặp số nguyên tố sinh đôi nhỏ hơn 40 là:
3 và 5
5 và 7
11 và 13
17 và 19
29 và 31.
a) Các số đó chia hết cho 5.
b) Các số đó chia hết cho 3.
Giải:
a) Số cần viết chia hết cho 5 nên nó có chữ số tận cùng là 0 hoặc 5. Vậy các số cần tìm là: 510; 150; 310; 130; 350; 530; 105; 305; 315; 135.
b) Số cần viết chia hết cho 3 nên tổng các chữ số của nó phải chia hết cho 3.
Từ các chữ số 5; 0; 1; 3, ta có hai cách nhóm thành bộ ba số có tổng chia hết cho 3:
5 + 0 + 1 = 6 chia hết cho 3.
5 + 1 + 3 = 9 chia hết cho 3.
Vậy các số cần tìm là: 501; 510; 105; 150; 513; 531; 135; 153; 351; 315.
Câu 2.26 - Trang 43:
Hãy phân tích các số A, B ra thừa số nguyên tố:
A = 42 . 63 ;
B = 92 . 152 .
Giải:

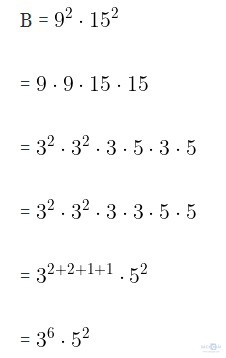
Bài tập 2.27 - Trang 43:
Tìm các số tự nhiên x không vượt quá 22 sao cho:
a) 100 – x chia hết cho 4.
b) 18 + 90 + x chia hết cho 9.
Giải:
a) Ta có: 100 – x chia hết cho 4. Mà 100 chia hết cho 4 nên x chia hết cho 4
Do đó x là bội của 4 và không vượt quá 22
Vậy x ∈ {0; 4; 8; 12; 16; 20}
b) Ta có: 18 + 90 + x chia hết cho 9. Mà 18 và 90 chia hết cho 9 nên x chia hết cho 9.
Do đó x là bội của 9 và không vượt quá 22
Vậy x ∈ {0; 9; 18}.
Bài tập 2.28 - Trang 43:
Lớp 6B có 40 học sinh. Để thực hiện dự án học tập nhỏ, cô giáo muốn chia lớp thành các nhóm có số người như nhau, mỗi nhóm nhiều hơn 3 người. Hỏi mỗi nhóm có thể có bao nhiêu người?
Giải:
Số người mỗi nhóm phải lớn hơn 3 và là ước của 40.
Mà Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}
Nên mỗi nhóm có thể có 4; 5; 8; 10; 20; hoặc 40 người.
Bài tập 2.29 - Trang 43:
Hai số nguyên tố được gọi là sinh đôi nếu chúng hơn kém nhau hai đơn vị. Ví dụ 17 và 19 là hai số nguyên tố sinh đôi. Em hãy liệt kê hết các cặp số nguyên tố sinh đôi nhỏ hơn 40.
Giải:
Các cặp số nguyên tố sinh đôi nhỏ hơn 40 là:
3 và 5
5 và 7
11 và 13
17 và 19
29 và 31.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025