Giải bài tập SGK Toán 6 bài 11: Số nguyên tố - Sách Kết nối tri thức với cuộc sống
Giải bài tập SGK Toán 6 bài 11: Số nguyên tố - Sách Kết nối tri thức với cuộc sống
Giải bài tập SGK Toán 6 bài 11: Số nguyên tố trang 44, 45, 46, 47, 48- Sách Kết nối tri thức với cuộc sống
Hoạt động 1 - Trang 44:
Tìm các tập hợp Ư(24) và Ư(28)
Giải:
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(28) = {1; 2; 4; 7; 14; 28}
Hoạt động 2 - Trang 44:
Gọi ƯC(24,28) là tập hợp các số vừa là ước của 24, vừa là ước của 28. Hãy viết tập hợp ƯC(24, 28)
Giải:
ƯC(24; 28) = {1; 2; 4}
Hoạt động 3 -Trang 44:
Tìm số lớn nhất trong tập ƯC(24, 28)
Giải:
Số lớn nhất trong ƯC(24; 28) là 4.
Luyện tập 1 - Trang 45:
Bố có 12 quả bóng màu xanh và 15 quả bóng màu đỏ. Bố muốn chia số bóng cho ba anh em Việt, Hà và Nam đều như nhau gồm cả bóng màu xanh và bóng màu đỏ. Hỏi Bố có thực hiện được điều đó hay không?
Giải:
Ta có: 3 ∈ Ư(12); 3 ∈ Ư(15)
Nên 3 ∈ ƯC(12; 15)
Do đó bố có thể thực hiện phép chia này.
Vận dụng 1 - Trang 45:
Tuần này lớp 6A và 6B gồm 40 học sinh nữ và 36 học sinh nam được phân công đi thu gom rác làm sạch bờ biển ở địa phương. Nếu chia nhóm sao cho số học sinh nam và nữ trong các nhóm bằng nhau thì:
a) Có thể chia được thành bao nhiêu nhóm học sinh?
b) Có thể chia nhiều nhất bao nhiêu nhóm học sinh?
Giải:
a) Gọi x là số nhóm học sinh chia được (x khác 1)
Khi đó x ∈ ƯC(36; 40)
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}
Vì x khác 1 nên x ∈ {2; 4}
b) Số nhóm chia được nhiều nhất là ƯCLN(36; 40) = 4
Luyện tập 2 - Trang 46:
Tìm ƯCLN(36, 84).
Giải:
36 = 22.22
84 = 22 . 3. 7
Ta thấy 2 và 3 là các thừa số nguyên tố chung của 36 và 84. Số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1 nên
ƯCLN(36; 84) = 22. 3 = 12
Vận dụng 2 -Trang 46:
Một đại đội bộ binh có ba trung đội: trung đội I có 24 chiến sĩ, trung đội II có 28 chiến sĩ, trung đội III có 36 chiến sĩ. Trong cuộc diễu binh, cả ba trung đội phải xếp thành các hàng dọc đều nhau mà không có chiến sĩ nào trong mỗi trung đội bị lẻ hàng. Hỏi có thể xếp được nhiều nhất bao nhiêu hàng dọc?
Giải:
Số hàng dọc nhiều nhất có thể xếp được là ƯCLN(24; 28; 36)
Ta có:
24 = 23.3
28 = 22.7
36 = 22. 32
Ta thấy 2 là thừa số nguyên tố chung của 24; 28 và 36. Số mũ nhỏ nhất của 2 là 22 nên ƯCLN(24; 28; 36) = 4
Vậy có thể xếp được 4 hàng dọc
Luyện tập 3 - Trang 48:
Rút gọn về phân số tối giản:
a.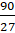
b.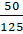
Giải:
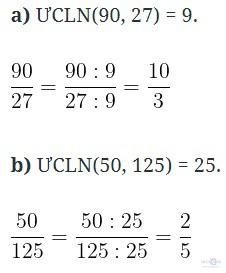
* BÀI TẬP
Câu 2.30 - Trang 48:
Tìm tập hợp ước chung của:
a) 30 và 45
b) 42 và 70
Giải:
a) Ta có:
30 = 2 . 3 . 5;
45 = 32 . 5
Các thừa số nguyên tố chung là 3 và 5. Số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1 nên:
ƯCLN(30, 45) = 3 . 5 = 15.
Các ước của 15 là 1; 3; 5; 15 nên:
ƯC(30, 45) = {1; 3; 5; 15}.
b) Ta có:
42 = 2 . 3 . 7
70 = 2 . 5 . 7
Các thừa số nguyên tố chung là 2 và 7. Số mũ nhỏ nhất của chúng đều là 1, nên:
ƯCLN(42, 70) = 2 . 7 = 14.
Các ước của 14 là: 1; 2; 7; 14. Vậy:
ƯC(42, 70) = {1; 2; 7; 14}.
Câu 2.31 - Trang 48:
Tìm ƯCLN của hai số:
a) 40 và 70
b) 55 và 77
Giải:
a) Ta có:
40 = 23 . 5
70 = 2 . 5 . 7
Các thừa số nguyên tố chung là 2 và 5. Số mũ nhỏ nhất của chúng đều bằng 1 nên:
ƯCLN(40, 70) = 2 . 5 = 10.
b) Ta có:
55 = 5 . 11
77 = 7 . 11
Thừa số nguyên tố chung là 11 với số mũ nhỏ nhất là 1, nên:
ƯCLN(55, 77) = 11.
Câu 2.32 - Trang 48:
Tìm ƯCLN của:
a) 22.5 và 2.3.5
b) 24.3; 22 . 32.5 và 24.11
Giải:
a) 22.5 và 2.3.5
Ta thấy 2 và 5 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 1 và số mũ nhỏ nhất của 5 là 1 nên
ƯCLN cần tìm là 2.5 = 10
b) 24.3; 22 . 32.5 và 24.11
Ta thấy 2 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 22 nên
ƯCLN cần tìm là 22 = 4
Câu 2.33 - Trang 48:
Cho hai số a = 72 và b = 96
a) Phân tích a và b ra thừa số nguyên tố
b) Tìm ƯCLN(a, b), rồi tìm ƯC(a, b)
Giải:
a) a = 72 = 23.32
b = 96 = 25.3
b) Ta thấy 2 và 3 là các thừa số chung của 70 và 96. Số mũ nhỏ nhất của 2 là 3 và số mũ nhỏ nhất của 3 là 1 nên
ƯCLN(72; 96) = 23.3 = 24
ƯC(a, b) = Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Câu 2.34 - Trang 48:
Các phân số sau đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản?
a) 5085
b) 2381
Giải:
a) Ta có:
50 = 2 . 52
85 = 5 . 17
Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1, nên:
ƯCLN(50, 85) = 5.
Do đó, phân số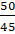 chưa phải là phân số tối giản. Ta có:
chưa phải là phân số tối giản. Ta có:
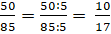
Ta được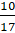 là phân số tối giản.
là phân số tối giản.
b) Ta có: ƯCLN(23, 81) = 1 nên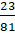 là phân số tối giản.
là phân số tối giản.
Câu 2.35 - Trang 48:
Hãy cho hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số
Giải:
Hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số:
4 và 9
8 và 27
Hoạt động 1 - Trang 44:
Tìm các tập hợp Ư(24) và Ư(28)
Giải:
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(28) = {1; 2; 4; 7; 14; 28}
Hoạt động 2 - Trang 44:
Gọi ƯC(24,28) là tập hợp các số vừa là ước của 24, vừa là ước của 28. Hãy viết tập hợp ƯC(24, 28)
Giải:
ƯC(24; 28) = {1; 2; 4}
Hoạt động 3 -Trang 44:
Tìm số lớn nhất trong tập ƯC(24, 28)
Giải:
Số lớn nhất trong ƯC(24; 28) là 4.
Luyện tập 1 - Trang 45:
Bố có 12 quả bóng màu xanh và 15 quả bóng màu đỏ. Bố muốn chia số bóng cho ba anh em Việt, Hà và Nam đều như nhau gồm cả bóng màu xanh và bóng màu đỏ. Hỏi Bố có thực hiện được điều đó hay không?
Giải:
Ta có: 3 ∈ Ư(12); 3 ∈ Ư(15)
Nên 3 ∈ ƯC(12; 15)
Do đó bố có thể thực hiện phép chia này.
Vận dụng 1 - Trang 45:
Tuần này lớp 6A và 6B gồm 40 học sinh nữ và 36 học sinh nam được phân công đi thu gom rác làm sạch bờ biển ở địa phương. Nếu chia nhóm sao cho số học sinh nam và nữ trong các nhóm bằng nhau thì:
a) Có thể chia được thành bao nhiêu nhóm học sinh?
b) Có thể chia nhiều nhất bao nhiêu nhóm học sinh?
Giải:
a) Gọi x là số nhóm học sinh chia được (x khác 1)
Khi đó x ∈ ƯC(36; 40)
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}
Vì x khác 1 nên x ∈ {2; 4}
b) Số nhóm chia được nhiều nhất là ƯCLN(36; 40) = 4
Luyện tập 2 - Trang 46:
Tìm ƯCLN(36, 84).
Giải:
36 = 22.22
84 = 22 . 3. 7
Ta thấy 2 và 3 là các thừa số nguyên tố chung của 36 và 84. Số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1 nên
ƯCLN(36; 84) = 22. 3 = 12
Vận dụng 2 -Trang 46:
Một đại đội bộ binh có ba trung đội: trung đội I có 24 chiến sĩ, trung đội II có 28 chiến sĩ, trung đội III có 36 chiến sĩ. Trong cuộc diễu binh, cả ba trung đội phải xếp thành các hàng dọc đều nhau mà không có chiến sĩ nào trong mỗi trung đội bị lẻ hàng. Hỏi có thể xếp được nhiều nhất bao nhiêu hàng dọc?
Giải:
Số hàng dọc nhiều nhất có thể xếp được là ƯCLN(24; 28; 36)
Ta có:
24 = 23.3
28 = 22.7
36 = 22. 32
Ta thấy 2 là thừa số nguyên tố chung của 24; 28 và 36. Số mũ nhỏ nhất của 2 là 22 nên ƯCLN(24; 28; 36) = 4
Vậy có thể xếp được 4 hàng dọc
Luyện tập 3 - Trang 48:
Rút gọn về phân số tối giản:
a.
b.
Giải:
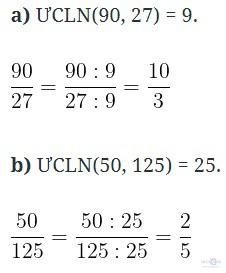
* BÀI TẬP
Câu 2.30 - Trang 48:
Tìm tập hợp ước chung của:
a) 30 và 45
b) 42 và 70
Giải:
a) Ta có:
30 = 2 . 3 . 5;
45 = 32 . 5
Các thừa số nguyên tố chung là 3 và 5. Số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1 nên:
ƯCLN(30, 45) = 3 . 5 = 15.
Các ước của 15 là 1; 3; 5; 15 nên:
ƯC(30, 45) = {1; 3; 5; 15}.
b) Ta có:
42 = 2 . 3 . 7
70 = 2 . 5 . 7
Các thừa số nguyên tố chung là 2 và 7. Số mũ nhỏ nhất của chúng đều là 1, nên:
ƯCLN(42, 70) = 2 . 7 = 14.
Các ước của 14 là: 1; 2; 7; 14. Vậy:
ƯC(42, 70) = {1; 2; 7; 14}.
Câu 2.31 - Trang 48:
Tìm ƯCLN của hai số:
a) 40 và 70
b) 55 và 77
Giải:
a) Ta có:
40 = 23 . 5
70 = 2 . 5 . 7
Các thừa số nguyên tố chung là 2 và 5. Số mũ nhỏ nhất của chúng đều bằng 1 nên:
ƯCLN(40, 70) = 2 . 5 = 10.
b) Ta có:
55 = 5 . 11
77 = 7 . 11
Thừa số nguyên tố chung là 11 với số mũ nhỏ nhất là 1, nên:
ƯCLN(55, 77) = 11.
Câu 2.32 - Trang 48:
Tìm ƯCLN của:
a) 22.5 và 2.3.5
b) 24.3; 22 . 32.5 và 24.11
Giải:
a) 22.5 và 2.3.5
Ta thấy 2 và 5 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 1 và số mũ nhỏ nhất của 5 là 1 nên
ƯCLN cần tìm là 2.5 = 10
b) 24.3; 22 . 32.5 và 24.11
Ta thấy 2 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 22 nên
ƯCLN cần tìm là 22 = 4
Câu 2.33 - Trang 48:
Cho hai số a = 72 và b = 96
a) Phân tích a và b ra thừa số nguyên tố
b) Tìm ƯCLN(a, b), rồi tìm ƯC(a, b)
Giải:
a) a = 72 = 23.32
b = 96 = 25.3
b) Ta thấy 2 và 3 là các thừa số chung của 70 và 96. Số mũ nhỏ nhất của 2 là 3 và số mũ nhỏ nhất của 3 là 1 nên
ƯCLN(72; 96) = 23.3 = 24
ƯC(a, b) = Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Câu 2.34 - Trang 48:
Các phân số sau đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản?
a) 5085
b) 2381
Giải:
a) Ta có:
50 = 2 . 52
85 = 5 . 17
Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1, nên:
ƯCLN(50, 85) = 5.
Do đó, phân số
Ta được
b) Ta có: ƯCLN(23, 81) = 1 nên
Câu 2.35 - Trang 48:
Hãy cho hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số
Giải:
Hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số:
4 và 9
8 và 27
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025