Giải Toán 8 sách Kết nối Tri Thức, bài: Luyện tập chung trang 40
Giải Toán 8 sách Kết nối Tri Thức, bài: Luyện tập chung trang 40.
Bài 2.16: Tính nhanh giá trị biểu thức
x2 + x +
x + 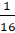 tại x = 99,75
tại x = 99,75
Giải:
Ta có x2 + x +
x + 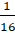 = x2 + 2. x .
= x2 + 2. x . +
+ 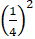 =
= 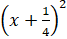 = (x + 0,25)2
= (x + 0,25)2
Thay x = 99,75 vào biểu thức (x + 0,25)2, ta được:
(99,75 + 0,25)2 = 1002 = 10 000.
Vậy tại x = 99,75 thì giá trị của biểu thức đã cho bằng 10 000.
Bài 2.17: Chứng minh đẳng thức (10a + 5)2 = 100a(a + 1) + 25. Từ đó em hãy nêu một quy tắc tính nhẩm bình phương của một số có tận cùng là 5.
Áp dụng: Tính 252; 352.
Giải:
Ta có (10a + 5)2 = (10a)2 + 2 . 10a . 5 + 52
= 100a2 + 100a + 25 = 100a(a + 1) + 25.
Từ đó ta rút ra quy tắc tính nhẩm bình phương của một số có tận cùng là 5 là:
Bình phương của một số tự nhiên có chữ số tận cùng là 5 bằng 100 lần tích của số tạo bởi các chữ số trước số tận cùng với số liền sau của số tạo bởi các chữ số trước số tận cùng rồi cộng với 25.
Áp dụng:
• 252 = (10 . 2 + 5)2 = 100 . 2 . (2 + 1) + 25 = 100 . 2 . 3 + 25
= 600 + 25 = 625;
• 352 = (10 . 3 + 5)2 = 100 . 3 . (3 + 1) + 25 = 100 . 3 . 4 + 25
= 1 200 + 25 = 1 225.
Bài 2.18: Tính nhanh giá trị của các biểu thức:
a) x3 + 3x2 + 3x + 1 tại x = 99;
b) x3 – 3x2y + 3xy2 – y3 tại x = 88 và y = –12.
Giải:
a) Ta có x3 + 3x2 + 3x + 1
= x3 + 3 . x2 . 1 + 3 . x . 12 + 13 = (x + 1)3.
Thay x = 99 vào biểu thức (x + 1)3, ta được:
(99 + 1)3 = 1003 = 1 000 000.
b) Ta có x3 – 3x2y + 3xy2 – y3 = (x – y)3.
Thay x = 88 và y = –12 vào biểu thức (x – y)3, ta được:
[88 – (–12)]3 = (88 + 12)3 = 1003 = 1 000 000.
Bài 2.19: Rút gọn các biểu thức:
a) (x – 2)3 + (x + 2)3 – 6x(x + 2)(x – 2);
b) (2x – y)3 + (2x + y)3.
Giải:
a) (x – 2)3 + (x + 2)3 – 6x(x + 2)(x – 2)
= [(x – 2) + (x + 2)] . [(x – 2)2 – (x – 2).(x + 2) + (x + 2)2] – 6x(x2 – 4)
= (x – 2 + x + 2).[x2 – 4x + 4 – (x2 – 4) + x2 + 4x + 4] – 6x(x2 – 4)
= 2x.(2x2 + 8 – x2 + 4) – 6x(x2 – 4)
= 2x(x2 + 12) – 6x(x2 – 4)
= 2x3 + 24x – 6x3 + 24x
= – 4x3 + 48x.
b) (2x – y)3 + (2x + y)3
= (2x)3 – 3 . (2x)2 . y + 3 . 2x . y2 – y3 + (2x)3 + 3 . (2x)2 . y + 3 . 2x . y2 + y3
= (2x)3 + 3 . 2x . y2 + (2x)3 + 3 . 2x . y2
= 8x3 + 6xy2 + 8x3 + 6xy2 = 16x3 + 12xy2.
Bài 2.20: Chứng minh rằng a3 + b3 = (a + b)3 – 3ab(a + b).
Áp dụng, tính a3 + b3 biết a + b = 4 và ab = 3.
Giải:
Ta có (a + b)3 = a3 + 3a2b + 3ab2 + b3
= a3 + 3ab(a + b) + b3
Do đó a3 + b3 = (a + b)3 – 3ab(a + b).
Áp dụng:
Với a + b = 4 và ab = 3, ta được:
a3 + b3 = (a + b)3 – 3ab(a + b)
= 43 – 3 . 3 . 4 = 64 – 36 = 28.
Bài 2.21: Bác Tùng gửi vào ngân hàng 200 triệu đồng theo thể thức lãi kép theo định kì với lãi suất x mỗi năm (tức là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp). Biểu thức S = 200(1+x)3 (triệu đồng) là số tiền bác Tùng nhận được sau 3 năm.
a) Tính số tiền bác Tùng nhận được sau 3 năm khi lãi suất x = 5,5%
b) Khai triển S thành đa thức theo x và xác định bậc của đa thức.
Giải:
a) Số tiền bác Tùng nhận được sau 3 năm khi lãi suất x = 5,5% là:
200 (1 + 0,055)3 = 234,8483 (triệu đồng)
b) S = 200 (1+x)3 = 200 (1 + 3x + 3x2 + x3)
=200 + 600x + 600x2 + 200x3
Đa thức S bậc 3
x2 +
Giải:
Ta có x2 +
Thay x = 99,75 vào biểu thức (x + 0,25)2, ta được:
(99,75 + 0,25)2 = 1002 = 10 000.
Vậy tại x = 99,75 thì giá trị của biểu thức đã cho bằng 10 000.
Bài 2.17: Chứng minh đẳng thức (10a + 5)2 = 100a(a + 1) + 25. Từ đó em hãy nêu một quy tắc tính nhẩm bình phương của một số có tận cùng là 5.
Áp dụng: Tính 252; 352.
Giải:
Ta có (10a + 5)2 = (10a)2 + 2 . 10a . 5 + 52
= 100a2 + 100a + 25 = 100a(a + 1) + 25.
Từ đó ta rút ra quy tắc tính nhẩm bình phương của một số có tận cùng là 5 là:
Bình phương của một số tự nhiên có chữ số tận cùng là 5 bằng 100 lần tích của số tạo bởi các chữ số trước số tận cùng với số liền sau của số tạo bởi các chữ số trước số tận cùng rồi cộng với 25.
Áp dụng:
• 252 = (10 . 2 + 5)2 = 100 . 2 . (2 + 1) + 25 = 100 . 2 . 3 + 25
= 600 + 25 = 625;
• 352 = (10 . 3 + 5)2 = 100 . 3 . (3 + 1) + 25 = 100 . 3 . 4 + 25
= 1 200 + 25 = 1 225.
Bài 2.18: Tính nhanh giá trị của các biểu thức:
a) x3 + 3x2 + 3x + 1 tại x = 99;
b) x3 – 3x2y + 3xy2 – y3 tại x = 88 và y = –12.
Giải:
a) Ta có x3 + 3x2 + 3x + 1
= x3 + 3 . x2 . 1 + 3 . x . 12 + 13 = (x + 1)3.
Thay x = 99 vào biểu thức (x + 1)3, ta được:
(99 + 1)3 = 1003 = 1 000 000.
b) Ta có x3 – 3x2y + 3xy2 – y3 = (x – y)3.
Thay x = 88 và y = –12 vào biểu thức (x – y)3, ta được:
[88 – (–12)]3 = (88 + 12)3 = 1003 = 1 000 000.
Bài 2.19: Rút gọn các biểu thức:
a) (x – 2)3 + (x + 2)3 – 6x(x + 2)(x – 2);
b) (2x – y)3 + (2x + y)3.
Giải:
a) (x – 2)3 + (x + 2)3 – 6x(x + 2)(x – 2)
= [(x – 2) + (x + 2)] . [(x – 2)2 – (x – 2).(x + 2) + (x + 2)2] – 6x(x2 – 4)
= (x – 2 + x + 2).[x2 – 4x + 4 – (x2 – 4) + x2 + 4x + 4] – 6x(x2 – 4)
= 2x.(2x2 + 8 – x2 + 4) – 6x(x2 – 4)
= 2x(x2 + 12) – 6x(x2 – 4)
= 2x3 + 24x – 6x3 + 24x
= – 4x3 + 48x.
b) (2x – y)3 + (2x + y)3
= (2x)3 – 3 . (2x)2 . y + 3 . 2x . y2 – y3 + (2x)3 + 3 . (2x)2 . y + 3 . 2x . y2 + y3
= (2x)3 + 3 . 2x . y2 + (2x)3 + 3 . 2x . y2
= 8x3 + 6xy2 + 8x3 + 6xy2 = 16x3 + 12xy2.
Bài 2.20: Chứng minh rằng a3 + b3 = (a + b)3 – 3ab(a + b).
Áp dụng, tính a3 + b3 biết a + b = 4 và ab = 3.
Giải:
Ta có (a + b)3 = a3 + 3a2b + 3ab2 + b3
= a3 + 3ab(a + b) + b3
Do đó a3 + b3 = (a + b)3 – 3ab(a + b).
Áp dụng:
Với a + b = 4 và ab = 3, ta được:
a3 + b3 = (a + b)3 – 3ab(a + b)
= 43 – 3 . 3 . 4 = 64 – 36 = 28.
Bài 2.21: Bác Tùng gửi vào ngân hàng 200 triệu đồng theo thể thức lãi kép theo định kì với lãi suất x mỗi năm (tức là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào vốn của kì kế tiếp). Biểu thức S = 200(1+x)3 (triệu đồng) là số tiền bác Tùng nhận được sau 3 năm.
a) Tính số tiền bác Tùng nhận được sau 3 năm khi lãi suất x = 5,5%
b) Khai triển S thành đa thức theo x và xác định bậc của đa thức.
Giải:
a) Số tiền bác Tùng nhận được sau 3 năm khi lãi suất x = 5,5% là:
200 (1 + 0,055)3 = 234,8483 (triệu đồng)
b) S = 200 (1+x)3 = 200 (1 + 3x + 3x2 + x3)
=200 + 600x + 600x2 + 200x3
Đa thức S bậc 3
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025