Giải Toán 8 sách Kết nối Tri Thức, bài 7: Lập phương của một tổng. Lập phương của một hiệu

Mở đầu trang 34: Chúng mình đã biết công thức (a + b)² = a² + 2ab + b², còn công thức tính (a + b)³ thì sao nhỉ?
Giải:
Ta đưa (a + b)³ về phép nhân đa thức:
(a + b)³ = (a + b)(a + b)².
 

1. Lập phương của một tổng

Hoạt động 1 trang 34: Với hai số a, b bất kì, thực hiện phép tính (a + b)(a + b)². Từ đó rút ra liên hệ giữa (a + b)³ và a³ + 3a²b + 3ab² + b³.
Giải:
Ta có (a + b)(a + b)² = (a + b)(a² + 2ab + b²)
= a³ + 2a²b + ab² + a²b + 2ab² + b³
= a³ + (2a²b + a²b) + (ab² + 2ab²) + b³
= a³ + 3a²b + 3ab² + b³.
Ta có (a + b)(a + b)² = (a + b)³; (a + b)(a + b)² = a³ + 3a²b + 3ab² + b³.
Vậy (a + b)3 = a³ + 3a²b + 3ab² + b³.

Luyện tập 1 trang 35: 
1. Khai triển
a) (x + 3)³;
b) (x + 2y)³.
2. Rút gọn biểu thức (2x + y)³ – 8x³ – y³.
Giải:
1.
a) (x + 3)³ = x³ + 3 . x² . 3 + 3 . x . 3² + 3³ = x³ + 9x² + 27x + 27;
b) (x + 2y)³ = x³ + 3 . x² . 2y + 3 . x . (2y)² + (2y)³
= x³ + 6x²y + 12xy² + 8y³.

2.
(2x + y)³ – 8x³ – y³
= (2x)³ + 3 . (2x)² . y + 3 . 2x . y² + y³ – 8x³ – y³
= 8x³ + 12x²y + 6xy² + y³ – 8x³ – y³
= (8x³ – 8x³) + 12x²y + 6xy² + (y³ – y³)
= 12x²y + 6xy².

Luyện tập 2 trang 35: Viết biểu thức x³ + 9x²y + 27xy² + 27y³ dưới dạng lập phương của một tổng.
Giải:
Ta có: x³ + 9x²y + 27xy² + 27y³
= x³ + 3x² . 3y + 3 . x . (3y)² + (3y)³
= (x + 3y)³.
Vậy x³ + 9x²y + 27xy² + 27y³ = (x + 3y)³.
 

2. Lập phương của một hiệu

Hoạt động 2 trang 35: Với hai số a, b bất kì, viết a – b = a + (–b) và áp dụng hằng đẳng thức lập phương của một tổng để tính (a – b)³.
Từ đó rút ra liên hệ giữa (a – b)³ và a³ – 3a²b + 3ab² – b³.
Giải:
(a – b)³ = [a + (–b)]³ = a³ + 3a³(−b) + 3a(−b)² + (–b)³
= a³ − 3a²b + 3ab² – b³.
Do đó (a – b)³ = a³ – 3a²b + 3ab² – b³.

Luyện tập 3 trang 35:
Khai triển (2x – y)³.
Giải:
Ta có (2x – y)³ = (2x)³ – 3 . (2x)² . y + 3 . 2x . y² – y³
= 8x³ – 12x²y + 6xy² – y³.

Luyện tập 4 trang 36: Viết biểu thức dưới dạng lập phương của một hiệu
8x³ – 36x²y + 54xy2 – 27y³.
Giải:
Ta có 8x³ – 36x²y + 54xy² – 27y³
= (2x)³ – 3 . (2x)² . 3y + 3 . (2x) . (3y)² – (3y)³
= (2x – 3y)³.

Vận dụng trang 36: Rút gọn biểu thức: (x – y)³ + (x + y)³.
Giải:
Ta có (x – y)³ + (x + y)³
= x³ – 3x2y + 3xy2 – y³ + x³ + 3x2y + 3xy2 + y³
= (x³ + x³) + (3x2y – 3x2y) + (3xy2 + 3xy2) + (y³ – y³)
= 2x³ + 6xy2.
 

3. Giải bài tập trang 36

Bài 2.7: Khai triển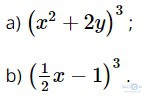

Giải:


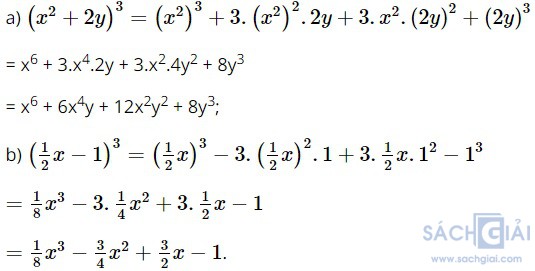
Bài 2.8: Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu.
a) 27 + 54x + 36x² + 8x³;
b) 64x³ – 144x²y + 108xy² – 27y³.
Giải:
a) 27 + 54x + 36x² + 8x³
= 3³ + 3 . 3² . 2x + 3 . 3 . (2x)² + (2x)³
= (3 + 2x)³;
b) 64x³ – 144x²y + 108xy² – 27y³
= (4x)³ – 3 . (4x)² . 3y + 3 . 4x . (3y)² – (3y)³
= (4x – 3y)³.

Bài 2.9: Tính nhanh giá trị của biểu thức:
a) x³ + 9x² + 27x + 27 tại x = 7;
b) 27 – 54x + 36x² – 8x³ tại x = 6,5.
Giải:
a) Ta có: x³ + 9x² + 27x + 27
= x³ + 3 . x² . 3 + 3 . x . 3² + 3³ = (x + 3)³.
Thay x = 7 vào biểu thức (x + 3)3, ta được:
(7 + 3)³ = 10³ = 1 000.
b) Ta có 27 – 54x + 36x² – 8x³
= 3³ – 3 . 3² . 2x + 3 . 3 . (2x)² – (2x)³
= (3 – 2x)³.
Thay x = 6,5 vào biểu thức (3 – 2x)³, ta được:
(3 – 2 . 6,5)³ = (3 – 13)³ = (–10)³ = –1 000.

Bài 2.10: Rút gọn các biểu thức sau:
a) (x – 2y)³ + (x + 2y)³;
b) (3x + 2y)³ + (3x – 2y)³.
Giải:
a) (x – 2y)³ + (x + 2y)³
= x³ – 3 . x² . 2y + 3 . x . (2y)2 – (2y)³ + x³ + 3 . x² . 2y + 3 . x . (2y)² + (2y)³
= x³ – 6x²y + 12xy²– 8y³ + x³ + 6x²y + 12xy²+ 8y³
= (x³ + x³) + (6x²y – 6x²y) + (12xy²+ 12xy²) + (8y³ – 8y³)
= 2x³ + 24xy².

b) (3x + 2y)³ + (3x – 2y)³
= (3x)³ + 3 . (3x)² . 2y + 3 . 3x . (2y)² + (2y)³ + (3x)³ – 3 . (3x)² . 2y + 3 . 3x . (2y)² – (2y)³
= (3x)³ + 3 . 3x . (2y)² + (3x)³ + 3 . 3x . (2y)²
= 27x³ + 36xy² + 27x³ + 36xy²
= 54x³ + 72xy².

Bài 2.11: Chứng minh (a – b)³ = – (b – a)³.
Giải:
Ta có
• (a – b)³ = a³ – 3a2b + 3ab² – b³;
• – (b – a)³ = – (b³ – 3b²a + 3ba² – a³)
= – b³ + 3b²a – 3ba² + a³ = a³ – 3a²b + 3ab² – b³.
Vậy (a – b)³ = – (b – a)³.