Giải Toán 8 sách Kết nối Tri Thức, bài: Bài tập cuối chương 1
Giải Toán 8 sách Kết nối Tri Thức, bài: Bài tập cuối chương 1 - Trang 27, 28.
A. Trắc Nghiệm
Bài 1.39: Đơn thức −23x2yz3 có:
A. hệ số -2, bậc 8
B. hệ số −23, bậc 5
C. hệ số -1, bậc 9
D. hệ số −23, bậc 6
Giải:
Đơn thức −23x2yz3 có hệ số là −23 và có bậc là: 2 + 1 + 3 = 6.
Đáp án: D
Bài 1.40: Gọi T là tổng, H là hiệu của hai đa thức 3x2y – 2xy2 + xy và –2x2y + 3xy2 + 1. Khi đó:
A. T = x2y – xy2 + xy + 1 và H = 5x2y – 5xy2 + xy – 1.
B. T = x2y + xy2 + xy + 1 và H = 5x2y – 5xy2 + xy – 1.
C. T = x2y + xy2 + xy + 1 và H = 5x2y – 5xy2 – xy – 1.
D. T = x2y + xy2 + xy – 1 và H = 5x2y + 5xy2 + xy – 1.
Giải:
Đáp án đúng là: B
Ta có:
• T = (3x2y – 2xy2 + xy) + (–2x2y + 3xy2 + 1)
= 3x2y – 2xy2 + xy – 2x2y + 3xy2 + 1
= (3x2y – 2x2y) + (3xy2 – 2xy2) + xy + 1
= x2y + xy2 + xy + 1.
• H = (3x2y – 2xy2 + xy) – (–2x2y + 3xy2 + 1)
= 3x2y – 2xy2 + xy + 2x2y – 3xy2 – 1
= (3x2y + 2x2y) – (3xy2 + 2xy2) + xy – 1
= 5x2y – 5xy2 + xy – 1.
Vậy T = x2y + xy2 + xy + 1; H = 5x2y – 5xy2 + xy – 1.
Bài 1.41: Tích của hai đơn thức 6x2yz và −2y2z2 là đơn thức
A. 4x2y3z3.
B. −12x2y3z3.
C. −12x3y3z3.
D. 4x3y3z3.
Giải:
Đáp án đúng là: B
Ta có 6x2yz . (−2y2z2) = [6 . (−2)] x2 (y . y2) (z . z2) = −12x2y3z3.
Vậy tích của hai đơn thức 6x2yz và −2y2z2 là đơn thức −12x2y3z3.
Bài 1.42: Khi chia đa thức 8x3y2 – 6x2y3 cho đơn thức −2xy, ta được kết quả là
A. −4x2y + 3xy2.
B. −4xy2 + 3x2y.
C. −10x2y + 4xy2.
D. −10x2y + 4xy2.
Lời giải:
Đáp án đúng là: A
Ta có (8x3y2 – 6x2y3) : (−2xy) = 8x3y2 : (−2xy) – 6x2y3 : (−2xy)
= −4x2y + 3xy2.
Vậy khi chia đa thức 8x3y2 – 6x2y3 cho đơn thức −2xy, ta được kết quả là −4x2y + 3xy2.
A. hệ số -2, bậc 8
B. hệ số −23, bậc 5
C. hệ số -1, bậc 9
D. hệ số −23, bậc 6
Giải:
Đơn thức −23x2yz3 có hệ số là −23 và có bậc là: 2 + 1 + 3 = 6.
Đáp án: D
Bài 1.40: Gọi T là tổng, H là hiệu của hai đa thức 3x2y – 2xy2 + xy và –2x2y + 3xy2 + 1. Khi đó:
A. T = x2y – xy2 + xy + 1 và H = 5x2y – 5xy2 + xy – 1.
B. T = x2y + xy2 + xy + 1 và H = 5x2y – 5xy2 + xy – 1.
C. T = x2y + xy2 + xy + 1 và H = 5x2y – 5xy2 – xy – 1.
D. T = x2y + xy2 + xy – 1 và H = 5x2y + 5xy2 + xy – 1.
Giải:
Đáp án đúng là: B
Ta có:
• T = (3x2y – 2xy2 + xy) + (–2x2y + 3xy2 + 1)
= 3x2y – 2xy2 + xy – 2x2y + 3xy2 + 1
= (3x2y – 2x2y) + (3xy2 – 2xy2) + xy + 1
= x2y + xy2 + xy + 1.
• H = (3x2y – 2xy2 + xy) – (–2x2y + 3xy2 + 1)
= 3x2y – 2xy2 + xy + 2x2y – 3xy2 – 1
= (3x2y + 2x2y) – (3xy2 + 2xy2) + xy – 1
= 5x2y – 5xy2 + xy – 1.
Vậy T = x2y + xy2 + xy + 1; H = 5x2y – 5xy2 + xy – 1.
Bài 1.41: Tích của hai đơn thức 6x2yz và −2y2z2 là đơn thức
A. 4x2y3z3.
B. −12x2y3z3.
C. −12x3y3z3.
D. 4x3y3z3.
Giải:
Đáp án đúng là: B
Ta có 6x2yz . (−2y2z2) = [6 . (−2)] x2 (y . y2) (z . z2) = −12x2y3z3.
Vậy tích của hai đơn thức 6x2yz và −2y2z2 là đơn thức −12x2y3z3.
Bài 1.42: Khi chia đa thức 8x3y2 – 6x2y3 cho đơn thức −2xy, ta được kết quả là
A. −4x2y + 3xy2.
B. −4xy2 + 3x2y.
C. −10x2y + 4xy2.
D. −10x2y + 4xy2.
Lời giải:
Đáp án đúng là: A
Ta có (8x3y2 – 6x2y3) : (−2xy) = 8x3y2 : (−2xy) – 6x2y3 : (−2xy)
= −4x2y + 3xy2.
Vậy khi chia đa thức 8x3y2 – 6x2y3 cho đơn thức −2xy, ta được kết quả là −4x2y + 3xy2.
B. Tự luận
Bài 1.43: Một đa thức hai biến bậc hai thu gọn có thể có nhiều nhất
a) bao nhiêu hạng tử bậc hai? Cho ví dụ.
b) bao nhiêu hạng tử bậc nhất? Cho ví dụ.
c) bao nhiêu hạng tử khác 0? Cho ví dụ.
Giải:
a) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 3 hạng tử bậc hai.
VD: -x2 + 2y2 – 7xy + 6, đa thức này có 3 hạng tử bậc hai là: -x2 ; 2y2 ; 7xy
b) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 2 hạng tử bậc nhất.
VD: 8xy + 2x + y, đa thức này có 2 hạng tử bậc nhất là: 2x và y
c) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 5 hạng tử khác 0
VD: 8x2 + 4y2 – xy – 5x + y - 1, đa thức này có 5 hạng tử khác 0 là 8x2 ; 4y2 ; xy ; 5x ; y
Bài 1.44: Cho biểu thức 3x3(x5 – y5) + y5(3x3 – y3).
a) Rút gọn biểu thức đã cho.
b) Tính giá trị của biểu thức đã cho nếu biết
y4 = x4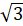
Giải:
a) Ta có 3x3(x5 – y5) + y5(3x3 – y3)
= 3x3 . x5 – 3x3 . y5 + y5 . 3x3 – y5 . y3
= 3x3 – 3x3y5 + 3x3y5 – y8 = 3x8 – y8.
b) Ta có y4 = x4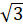 suy ra (y4)2 =
suy ra (y4)2 = 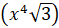 2 hay y8 = 3x8.
2 hay y8 = 3x8.
Thay y8 = 3x8 vào biểu thức 3x8 – y8, ta được: 3x8 – 3x8 = 0.
Vậy nếu y4 = x4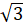 thì giá trị của biểu thức đã cho bằng 0.
thì giá trị của biểu thức đã cho bằng 0.
Bài 1.45: Rút gọn biểu thức
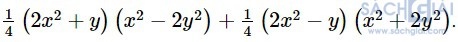
Giải:
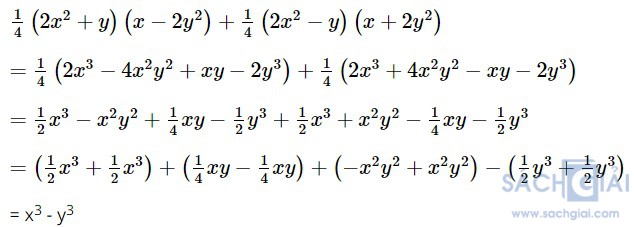
Bài 1.46: Bạn Thành dùng một miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) bằng cách cắt bốn hình vuông cạnh x cm ở bốn góc (H.1.3) rồi gấp lại. Biết rằng miếng bìa có chiều dài là y cm, chiều rộng là z cm
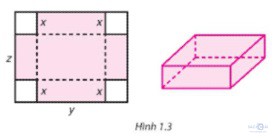
Tìm đa thức (ba biến x, y, z) biểu thị thể tích của chiếc hộp. Xác định bậc của đa thức đó
Giải:
Cắt miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) thì chiếc hộp có:
• Chiều dài là: y – 2x (cm)
• Chiều rộng là: z – 2x (cm)
• Chiều cao là: x (cm)
Đa thức biểu thị thể tích của chiếc hộp là:
x(y – 2x)(z – 2x) = (xy – 2x2)(z – 2x) = xyz – 2x2y – 2x2z + 4x3.
Đa thức xyz – 2x2y – 2x2z + 4x3 có bậc là 3.
Bài 1.47: Biết rằng D là một đơn thức sao cho –2x3y4 : D = xy2. Hãy tìm thương của phép chia:
(10x5y2 – 6x3y4 + 8x2y5) : D.
Giải:
Ta có –2x3y4 : D = xy2.
Suy ra D = –2x3y4 : xy2 = –2x2y2.
Khi đó, (10x5y2 – 6x3y4 + 8x2y5) : D
= (10x5y2 – 6x3y4 + 8x2y5) : (–2x2y2)
= 10x5y2 : (–2x2y2) – 6x3y4 : (–2x2y2) + 8x2y5 : (–2x2y2)
= –5x3 + 3xy2 – 4y3.
Vậy (10x5y2 – 6x3y4 + 8x2y5) : D = –5x3 + 3xy2 – 4y3.
Bài 1.48: Làm phép chia sau theo hướng dẫn:Làm phép chia sau theo hướng dẫn:
[8x3(2x – 5)2 – 6x2(2x – 5)3 + 10x(2x – 5)2] : 2x(2x – 5)2.
Hướng dẫn: Đặt y = 2x – 5.
Giải:
Đặt y = 2x – 5.
Khi đó, ta có [8x3(2x – 5)2 – 6x2(2x – 5)3 + 10x( – 5)2] : 2x(2x – 5)2
= (8x3y2 – 6x2y3 + 10xy2) : 2xy2
= 8x3y2 : 2xy2 – 6x2y3 : 2xy2 + 10xy2 : 2xy2
= 4x2 – 3xy + 5 = 4x2 – 3x(2x – 5) + 5
= 4x2 – 6x2 + 15x + 5 = – 2x2 + 15x + 5.
Vậy [8x3(2x – 5)2 – 6x2(2x – 5)3 + 10x(2x – 5)2] : 2x(2x – 5)2 = – 2x2 + 15x + 5
a) bao nhiêu hạng tử bậc hai? Cho ví dụ.
b) bao nhiêu hạng tử bậc nhất? Cho ví dụ.
c) bao nhiêu hạng tử khác 0? Cho ví dụ.
Giải:
a) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 3 hạng tử bậc hai.
VD: -x2 + 2y2 – 7xy + 6, đa thức này có 3 hạng tử bậc hai là: -x2 ; 2y2 ; 7xy
b) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 2 hạng tử bậc nhất.
VD: 8xy + 2x + y, đa thức này có 2 hạng tử bậc nhất là: 2x và y
c) Một đa thức hai biến bậc hai thu gọn có thể nhiều nhất 5 hạng tử khác 0
VD: 8x2 + 4y2 – xy – 5x + y - 1, đa thức này có 5 hạng tử khác 0 là 8x2 ; 4y2 ; xy ; 5x ; y
Bài 1.44: Cho biểu thức 3x3(x5 – y5) + y5(3x3 – y3).
a) Rút gọn biểu thức đã cho.
b) Tính giá trị của biểu thức đã cho nếu biết
y4 = x4
Giải:
a) Ta có 3x3(x5 – y5) + y5(3x3 – y3)
= 3x3 . x5 – 3x3 . y5 + y5 . 3x3 – y5 . y3
= 3x3 – 3x3y5 + 3x3y5 – y8 = 3x8 – y8.
b) Ta có y4 = x4
Thay y8 = 3x8 vào biểu thức 3x8 – y8, ta được: 3x8 – 3x8 = 0.
Vậy nếu y4 = x4
Bài 1.45: Rút gọn biểu thức
Giải:
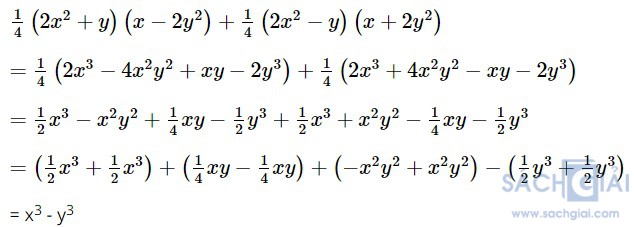
Bài 1.46: Bạn Thành dùng một miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) bằng cách cắt bốn hình vuông cạnh x cm ở bốn góc (H.1.3) rồi gấp lại. Biết rằng miếng bìa có chiều dài là y cm, chiều rộng là z cm

Tìm đa thức (ba biến x, y, z) biểu thị thể tích của chiếc hộp. Xác định bậc của đa thức đó
Giải:
Cắt miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) thì chiếc hộp có:
• Chiều dài là: y – 2x (cm)
• Chiều rộng là: z – 2x (cm)
• Chiều cao là: x (cm)
Đa thức biểu thị thể tích của chiếc hộp là:
x(y – 2x)(z – 2x) = (xy – 2x2)(z – 2x) = xyz – 2x2y – 2x2z + 4x3.
Đa thức xyz – 2x2y – 2x2z + 4x3 có bậc là 3.
Bài 1.47: Biết rằng D là một đơn thức sao cho –2x3y4 : D = xy2. Hãy tìm thương của phép chia:
(10x5y2 – 6x3y4 + 8x2y5) : D.
Giải:
Ta có –2x3y4 : D = xy2.
Suy ra D = –2x3y4 : xy2 = –2x2y2.
Khi đó, (10x5y2 – 6x3y4 + 8x2y5) : D
= (10x5y2 – 6x3y4 + 8x2y5) : (–2x2y2)
= 10x5y2 : (–2x2y2) – 6x3y4 : (–2x2y2) + 8x2y5 : (–2x2y2)
= –5x3 + 3xy2 – 4y3.
Vậy (10x5y2 – 6x3y4 + 8x2y5) : D = –5x3 + 3xy2 – 4y3.
Bài 1.48: Làm phép chia sau theo hướng dẫn:Làm phép chia sau theo hướng dẫn:
[8x3(2x – 5)2 – 6x2(2x – 5)3 + 10x(2x – 5)2] : 2x(2x – 5)2.
Hướng dẫn: Đặt y = 2x – 5.
Giải:
Đặt y = 2x – 5.
Khi đó, ta có [8x3(2x – 5)2 – 6x2(2x – 5)3 + 10x( – 5)2] : 2x(2x – 5)2
= (8x3y2 – 6x2y3 + 10xy2) : 2xy2
= 8x3y2 : 2xy2 – 6x2y3 : 2xy2 + 10xy2 : 2xy2
= 4x2 – 3xy + 5 = 4x2 – 3x(2x – 5) + 5
= 4x2 – 6x2 + 15x + 5 = – 2x2 + 15x + 5.
Vậy [8x3(2x – 5)2 – 6x2(2x – 5)3 + 10x(2x – 5)2] : 2x(2x – 5)2 = – 2x2 + 15x + 5
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025