Giải SGK Toán 7 sách Kết nối tri thức, bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Giải SGK Toán 7 sách Kết nối tri thức, bài 16: Tam giác cân. Đường trung trực của đoạn thẳng - Trang 80, ...
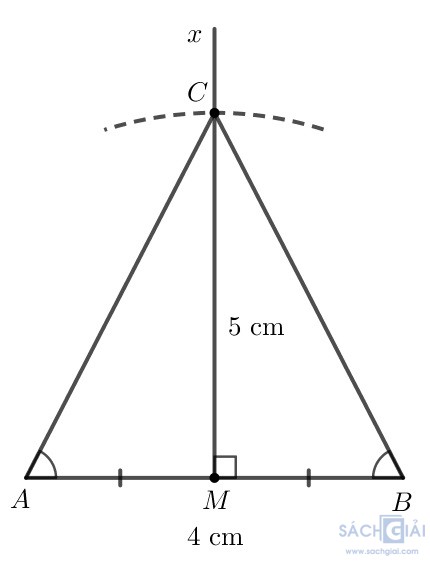
Mở đầu trang 80: Kiến trúc sư vẽ bản thiết kế ngôi nhà hình tam giác theo tỉ lệ 1 : 100. Biết rằng ngôi nhà cao 5 m, bề ngang mặt sàn rộng 4 m và hai mái nghiêng như nhau. Theo em, bản thiết kế làm thế nào để xác định được chính xác điểm C thể hiện đỉnh ngôi nhà?
Kiến trúc sư vẽ bản thiết kế ngôi nhà hình tam giác theo tỉ lệ 1 : 100
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Giải:
Điểm C cần dựng là điểm thỏa mãn cách đoạn thẳng AB một đoạn bằng 5cm và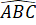 =
= 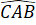 (2 mái nghiêng như nhau). Do đó C nằm trên đường trung trực của đoạn thẳng AB.
(2 mái nghiêng như nhau). Do đó C nằm trên đường trung trực của đoạn thẳng AB.
Cách dựng như sau:
Bước 1. Lấy điểm M là trung điểm của đoạn AB.
Bước 2. Kẻ tia Mx vuông góc với AB tại M.
Bước 3. Vẽ đường tròn tâm M, bán kính 5 cm, đường tròn cắt tia Mx tại điểm C.
Chứng minh:
Điểm C thỏa mãn cách đoạn thẳng AB một đoạn bằng 5cm.
Xét tam giác CMA vuông tại M và tam giác CMB vuông tại M có:
AM = MB (theo cách dựng).
CM chung.
Suy ra ΔCMA = ΔCMB (2 cạnh góc vuông).
Do đó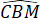 =
= 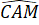 (2 góc tương ứng) hay
(2 góc tương ứng) hay 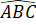 =
= 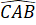
Kiến trúc sư vẽ bản thiết kế ngôi nhà hình tam giác theo tỉ lệ 1 : 100
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Giải:
Điểm C cần dựng là điểm thỏa mãn cách đoạn thẳng AB một đoạn bằng 5cm và
Cách dựng như sau:
Bước 1. Lấy điểm M là trung điểm của đoạn AB.
Bước 2. Kẻ tia Mx vuông góc với AB tại M.
Bước 3. Vẽ đường tròn tâm M, bán kính 5 cm, đường tròn cắt tia Mx tại điểm C.

Chứng minh:
Điểm C thỏa mãn cách đoạn thẳng AB một đoạn bằng 5cm.
Xét tam giác CMA vuông tại M và tam giác CMB vuông tại M có:
AM = MB (theo cách dựng).
CM chung.
Suy ra ΔCMA = ΔCMB (2 cạnh góc vuông).
Do đó
1. Tam giác cân và tính chất
Câu hỏi trang 80: Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam giác cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
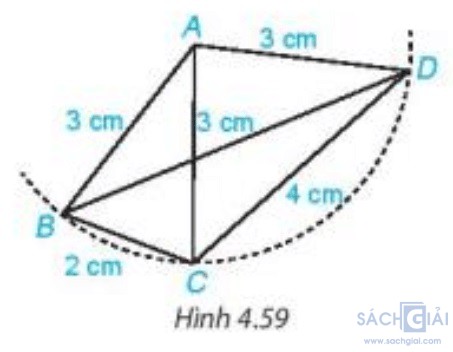
Giải:
Tam giác ABC có AB = AC = 3 cm nên tam giác ABC cân tại A.
Trong tam giác cân ABC có:
Cạnh bên: AB, AC.
Cạnh đáy: BC.
Góc ở đỉnh: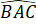
Góc ở đáy: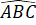 ,
, 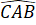
Tam giác ADC có AD = AC = 3 cm nên tam giác ADC cân tại A.
Trong tam giác cân ADC có:
Cạnh bên: AD, AC.
Cạnh đáy: CD.
Góc ở đỉnh: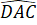
Góc ở đáy: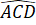 ,
, 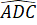
Tam giác ABD có AB = AD = 3 cm nên tam giác ABD cân tại A.
Trong tam giác cân ABD có:
Cạnh bên: AB, AD.
Cạnh đáy: BD.
Góc ở đỉnh: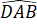
Góc ở đáy: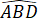 ,
, 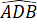
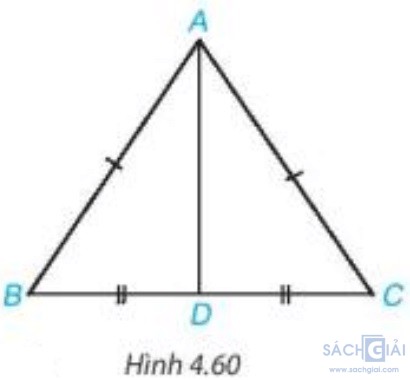
Hoạt động 1 - Trang 81: Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
a) Chứng minh rằng ΔABD = ΔACD theo trường hợp cạnh – cạnh – cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
Giải:
a) Xét hai tam giác ABD và ACD có:
AB = AC (do tam giác ABC cân tại A).
AD chung.
BD = CD (do D là trung điểm của đoạn thẳng BC).
Vậy ΔABD = ΔACD (cạnh – cạnh – cạnh).
b) Do ΔABD = ΔACD nên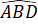 =
= 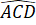 hay
hay 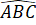 =
= 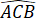
Vậy hai góc B và C của tam giác ABC bằng nhau.
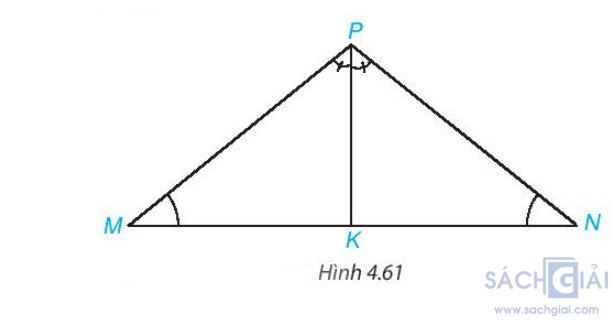
Hoạt động 2 - Trang 81: Cho tam giác MNP có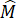 =
= 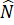
Vẽ tia phân giác PK của góc MPN ( K ∈ MN).
Chứng minh rằng:
a)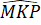 =
= 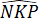
b) ΔMPK = ΔNPK;
c) Tam giác MNP có cân tại P không?
Giải:
a) Xét tam giác MPK có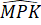 +
+ 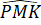 +
+ 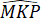 = 180o
= 180o
Do đó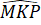 = 180o -
= 180o - 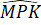 -
- 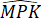 (1)
(1)
Xét tam giác NPK có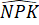 +
+ 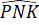 +
+ 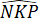 = 180o
= 180o
Do đó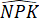 = 180o -
= 180o - 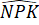 -
- 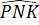 (2)
(2)
Mà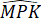 =
= 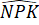 (do PK là tia phân giác của góc MPN) và
(do PK là tia phân giác của góc MPN) và 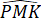 +
+ 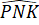 (theo giả thiết) nên từ (1) và (2) có
(theo giả thiết) nên từ (1) và (2) có 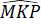 =
= 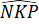
b) Xét hai tam giác MPK và NPK có:
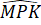 =
= 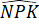 (do PK là tia phân giác của góc MPN).
(do PK là tia phân giác của góc MPN).
PK chung.
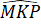 =
= 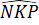 (chứng minh trên).
(chứng minh trên).
Vậy ΔMPK = ΔNPK (g – c – g).
c) Do ΔMPK = ΔNPK
nên PM = PN (2 cạnh tương ứng).
Tam giác MNP có PM = PN (chứng minh trên) nên tam giác MNP cân tại P.
Vậy tam giác MNP cân tại P.
Luyện tập 1 - Trang 81: Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
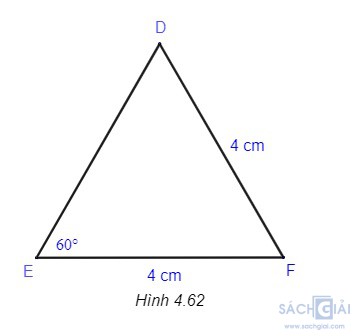
Giải:

Thử thách nhỏ trang 81: Một tam giác có gì đặc biệt nếu thỏa mãn một trong các điều kiện sau:
a) Tam giác có ba góc bằng nhau.
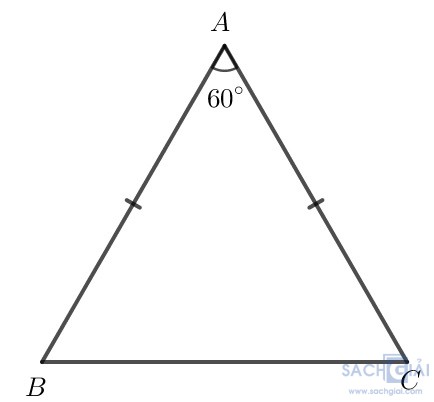
b) Tam giác cân có một góc bằng 60o.
Giải:
a.
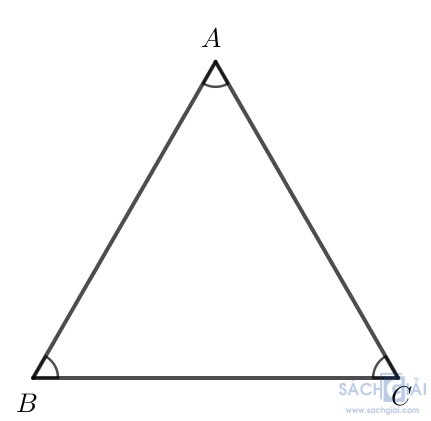
Xét tam giác ABC có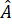 =
= 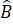 nên tam giác ABC cân tại C.
nên tam giác ABC cân tại C.
Do đó AC = BC (1).
Xét tam giác ABC có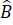 =
= 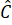 nên tam giác ABC cân tại A.
nên tam giác ABC cân tại A.
Do đó AB = AC (2).
Từ (1) và (2) có AB = BC = AC.
Lại có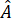 =
= 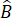 =
= 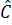 nên tam giác ABC là tam giác đều.
nên tam giác ABC là tam giác đều.
Vậy tam giác có ba góc bằng nhau là tam giác đều.
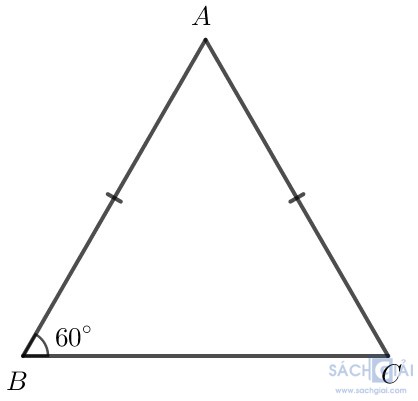
b.Trường hợp 1. Xét góc 60o là góc ở đỉnh.



Giải:
Tam giác ABC có AB = AC = 3 cm nên tam giác ABC cân tại A.
Trong tam giác cân ABC có:
Cạnh bên: AB, AC.
Cạnh đáy: BC.
Góc ở đỉnh:
Góc ở đáy:
Tam giác ADC có AD = AC = 3 cm nên tam giác ADC cân tại A.
Trong tam giác cân ADC có:
Cạnh bên: AD, AC.
Cạnh đáy: CD.
Góc ở đỉnh:
Góc ở đáy:
Tam giác ABD có AB = AD = 3 cm nên tam giác ABD cân tại A.
Trong tam giác cân ABD có:
Cạnh bên: AB, AD.
Cạnh đáy: BD.
Góc ở đỉnh:
Góc ở đáy:
Hoạt động 1 - Trang 81: Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
a) Chứng minh rằng ΔABD = ΔACD theo trường hợp cạnh – cạnh – cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?

Giải:
a) Xét hai tam giác ABD và ACD có:
AB = AC (do tam giác ABC cân tại A).
AD chung.
BD = CD (do D là trung điểm của đoạn thẳng BC).
Vậy ΔABD = ΔACD (cạnh – cạnh – cạnh).
b) Do ΔABD = ΔACD nên
Vậy hai góc B và C của tam giác ABC bằng nhau.
Hoạt động 2 - Trang 81: Cho tam giác MNP có
Vẽ tia phân giác PK của góc MPN ( K ∈ MN).
Chứng minh rằng:
a)
b) ΔMPK = ΔNPK;
c) Tam giác MNP có cân tại P không?

Giải:
a) Xét tam giác MPK có
Do đó
Xét tam giác NPK có
Do đó
Mà
b) Xét hai tam giác MPK và NPK có:
PK chung.
Vậy ΔMPK = ΔNPK (g – c – g).
c) Do ΔMPK = ΔNPK
nên PM = PN (2 cạnh tương ứng).
Tam giác MNP có PM = PN (chứng minh trên) nên tam giác MNP cân tại P.
Vậy tam giác MNP cân tại P.
Luyện tập 1 - Trang 81: Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.

Giải:

Thử thách nhỏ trang 81: Một tam giác có gì đặc biệt nếu thỏa mãn một trong các điều kiện sau:
a) Tam giác có ba góc bằng nhau.
b) Tam giác cân có một góc bằng 60o.
Giải:
a.

Xét tam giác ABC có
Do đó AC = BC (1).
Xét tam giác ABC có
Do đó AB = AC (2).
Từ (1) và (2) có AB = BC = AC.
Lại có
Vậy tam giác có ba góc bằng nhau là tam giác đều.
b.Trường hợp 1. Xét góc 60o là góc ở đỉnh.




2. Đường trung trực của một đoạn thẳng
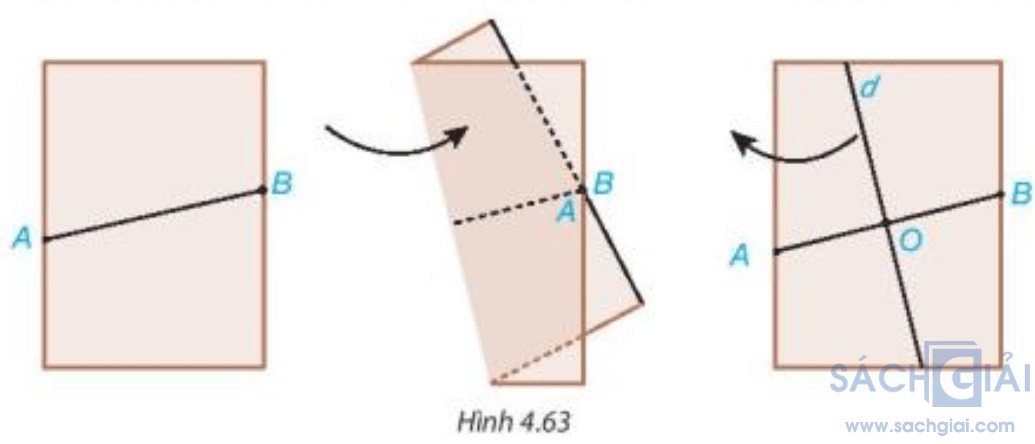
Hoạt động 3 - Trang 81: Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB.
Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau.
Mở mảnh giấy ra, kẻ đường thẳng d theo nếp gấp.
a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?
b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?
Giải:
a) Dùng thước thẳng có vạch chia ta đo được OA = OB nên O là trung điểm của đoạn thẳng AB.
b) Dùng thước đo góc, ta đo được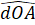 = 90o
= 90o
Vậy d vuông góc với AB.
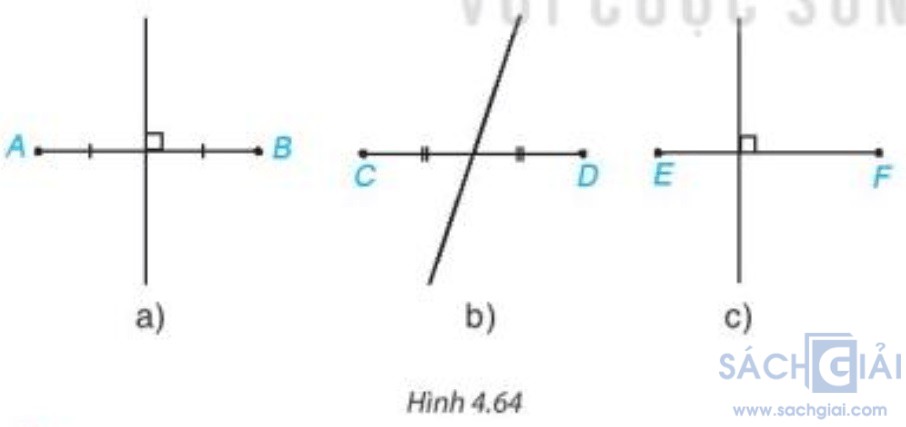
Câu hỏi trang 82: Trong Hình 4.64, bạn Lan vẽ đường trung trực của các đoạn thẳng. Theo em, hình nào Lan vẽ đúng?
Giải:
a) Đường thẳng trong hình vuông góc với AB tại trung điểm của AB nên là đường trung trực của đoạn AB.
b) Đường thẳng trong hình đi qua trung điểm của CD nhưng không vuông góc.
Do đó đường thẳng này không phải đường trung trực của đoạn CD.
c) Đường thẳng trong hình không vuông góc với EF tại trung điểm của EF.
Do đó đường thẳng này không phải đường trung trực của đoạn EF.
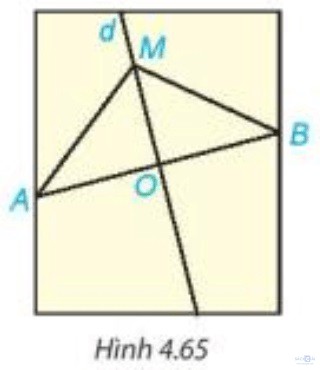
Hoạt động 4 - Trang 82: Trên mảnh giấy trong Hoạt động 3, lấy điểm M bất kì trên đường thẳng d. Dùng thước thẳng có vạch chia kiểm tra xem AM có bằng BM không (H.4.65).
Giải:
Dùng thước thẳng có vạch chia ta đo được AM = BM.
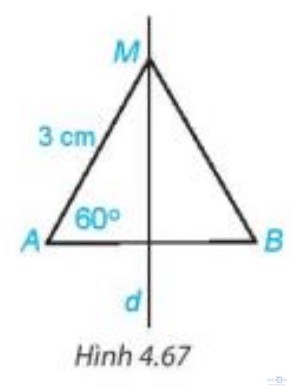
Luyện tập 2 trang 83 Toán lớp 7 Tập 1: Cho M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Biết AM = 3 cm và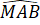 = 60o (H.4.67). Tính BM và số đo góc MBA.
= 60o (H.4.67). Tính BM và số đo góc MBA.
Giải:
Do M nằm trên đường trung trực của AB nên MA = MB = 3 cm.
Tam giác MAB có MA = MB nên tam giác MAB cân tại M.;
Do đó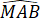 =
= 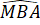 = 60o
= 60o
Vậy BM = 3 cm,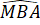 = 60o
= 60o
Thực hành trang 83: Sử dụng thước thẳng và compa để vẽ đường trung trực của đoạn thẳng AB như sau:
- Vẽ đoạn thẳng AB;
- Lấy A làm tâm, vẽ cung tròn (bán kính lớn hơn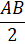 ), sau đó lấy B làm tâm, vẽ cung tròn có cùng bán kính, sao cho hai cung tròn này cắt nhau tại hai điểm M và N;
), sau đó lấy B làm tâm, vẽ cung tròn có cùng bán kính, sao cho hai cung tròn này cắt nhau tại hai điểm M và N;
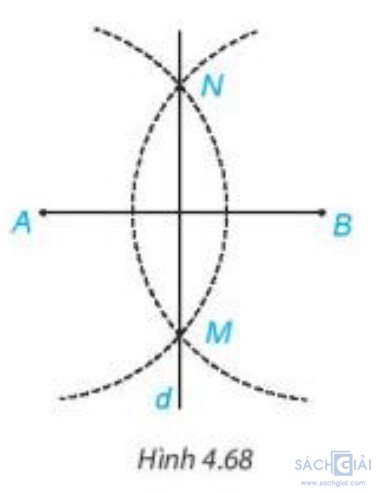
- Dùng thước thẳng vẽ đường thẳng MN. Khi đó MN là đường trung trực của đoạn thẳng AB (H.4.68).
Giải:
Thực hiện vẽ theo các bước như sau:
Bước 1. Vẽ đoạn thẳng AB (giả sử AB = 4 cm).
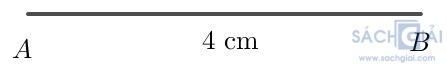
Bước 2. Khi đó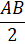 = 2cm
= 2cm
Từ A vẽ cung tròn tâm A bán kính 3 cm (tùy ý).
Từ B vẽ cung tròn tâm B bán kính 3 cm.
Hai cung tròn này cắt nhau tại M và N.
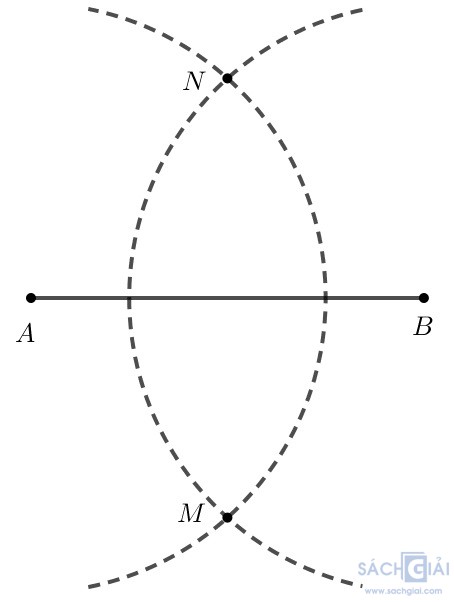
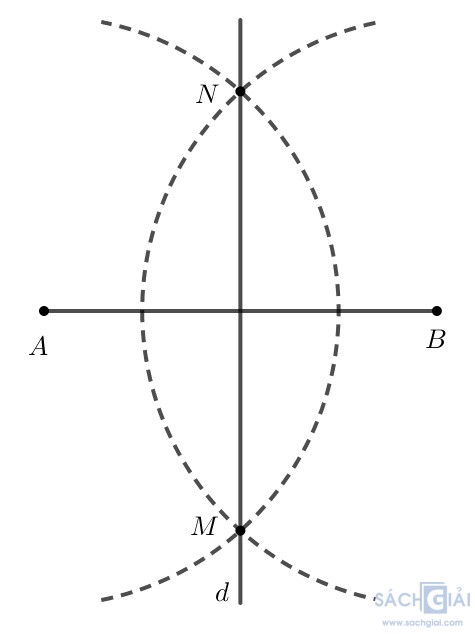
Bước 3. Dùng thước thẳng vẽ đường thẳng MN. Khi đó MN là đường trung trực của đoạn thẳng AB.
Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau.
Mở mảnh giấy ra, kẻ đường thẳng d theo nếp gấp.
a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?
b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?

Giải:
a) Dùng thước thẳng có vạch chia ta đo được OA = OB nên O là trung điểm của đoạn thẳng AB.
b) Dùng thước đo góc, ta đo được
Vậy d vuông góc với AB.
Câu hỏi trang 82: Trong Hình 4.64, bạn Lan vẽ đường trung trực của các đoạn thẳng. Theo em, hình nào Lan vẽ đúng?

Giải:
a) Đường thẳng trong hình vuông góc với AB tại trung điểm của AB nên là đường trung trực của đoạn AB.
b) Đường thẳng trong hình đi qua trung điểm của CD nhưng không vuông góc.
Do đó đường thẳng này không phải đường trung trực của đoạn CD.
c) Đường thẳng trong hình không vuông góc với EF tại trung điểm của EF.
Do đó đường thẳng này không phải đường trung trực của đoạn EF.
Hoạt động 4 - Trang 82: Trên mảnh giấy trong Hoạt động 3, lấy điểm M bất kì trên đường thẳng d. Dùng thước thẳng có vạch chia kiểm tra xem AM có bằng BM không (H.4.65).

Giải:
Dùng thước thẳng có vạch chia ta đo được AM = BM.
Luyện tập 2 trang 83 Toán lớp 7 Tập 1: Cho M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Biết AM = 3 cm và

Giải:
Do M nằm trên đường trung trực của AB nên MA = MB = 3 cm.
Tam giác MAB có MA = MB nên tam giác MAB cân tại M.;
Do đó
Vậy BM = 3 cm,
Thực hành trang 83: Sử dụng thước thẳng và compa để vẽ đường trung trực của đoạn thẳng AB như sau:
- Vẽ đoạn thẳng AB;
- Lấy A làm tâm, vẽ cung tròn (bán kính lớn hơn
- Dùng thước thẳng vẽ đường thẳng MN. Khi đó MN là đường trung trực của đoạn thẳng AB (H.4.68).

Giải:
Thực hiện vẽ theo các bước như sau:
Bước 1. Vẽ đoạn thẳng AB (giả sử AB = 4 cm).
Bước 2. Khi đó
Từ A vẽ cung tròn tâm A bán kính 3 cm (tùy ý).
Từ B vẽ cung tròn tâm B bán kính 3 cm.
Hai cung tròn này cắt nhau tại M và N.

Bước 3. Dùng thước thẳng vẽ đường thẳng MN. Khi đó MN là đường trung trực của đoạn thẳng AB.

3. Giải bài tập SGK trang 84
Bài 4.23 - Trang 84: Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
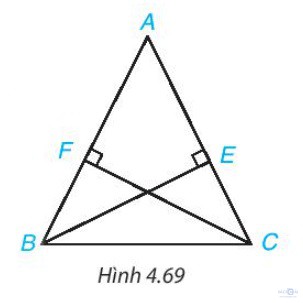
Giải:
Do tam giác ABC cân tại A nên: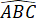 =
= 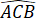 (tính chất tam giác cân)
(tính chất tam giác cân)
Xét 2 tam giác vuông BFC và CEB:
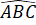 =
= 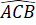
BC chung
=> ΔBFC = ΔCEB (cạnh huyền – góc nhọn)
=>BE = CF (2 cạnh tương ứng).
Bài 4.24 - Trang 84: Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
Giải:
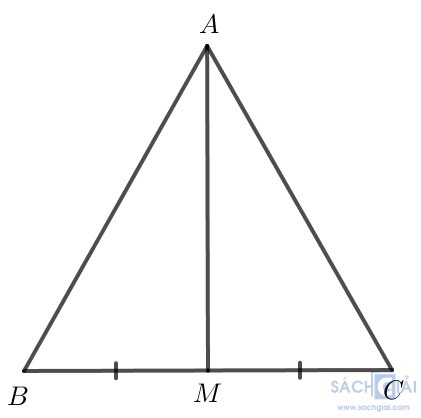

Bài 4.25 - Trang 84: Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
Giải:
a.
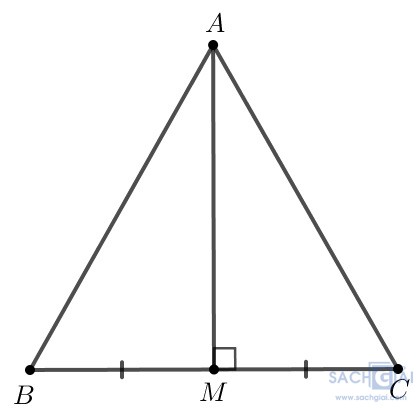
Do M là trung điểm của BC nên MB = MC.
Do AM⊥BC nên tam giác AMB vuông tại M, tam giác AMC vuông tại M.
Xét hai tam giác AMB vuông tại M và AMC vuông tại M có:
AM chung.
MB = MC (chứng minh trên).
Do đó ΔAMB = ΔAMC (2 cạnh góc vuông).
Khi đó AB = AC (2 cạnh tương ứng).
Tam giác ABC có AB = AC nên tam giác ABC cân tại A.
Vậy tam giác ABC cân tại A.
b)
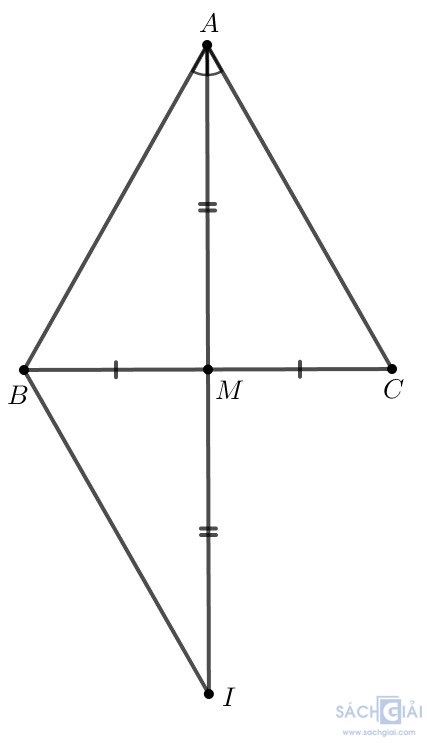

Bài 4.26 - Trang 84: Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân.
Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng 45°;
c) Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
Giải:
a. Dựa vào định lý tổng ba góc trong 1 tam giác bằng180° => tam giác không thể có 2 góc vuông
=>Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau
=> Tam giác vuông cân thì cân tại đỉnh góc vuông.
b. Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau => Tổng hai góc nhọn sẽ bằng : 180° - 90° = 90°
=> Mỗi góc nhọn sẽ là 45°
Vậy tam giác vuông cân có hai góc nhọn bằng 45°.
c. Áp dụng định lý tổng ba góc trong 1 tam giác bằng 180° , ta có số đo góc còn lại là : 180° - 90° - 45° = 45°
Vậy tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
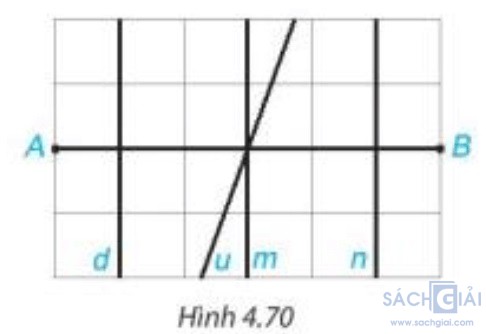
Bài 4.27 - Trang 84: Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB?
Giải:
Trong Hình 4.70, ta thấy đường thẳng m vuông góc với AB tại trung điểm của AB nên đường thẳng m là đường trung trực của đoạn thẳng AB.
Bài 4.27 - Trang 84: Cho tam giác ABC cân tại A có đường cao AD. Chứng minh rằng đường thẳng AD là đường trung trực của đoạn thẳng BC.
Giải:
Do tam giác ABC cân tại A nên AB = AC,
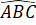 =
= 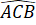
hay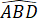 =
= 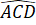
Do AD là đường cao của tam giác ABC hay AD ⊥ BC tại D nên tam giác ABD vuông tại D và tam giác ACD vuông tại D.
Xét hai tam giác ABD vuông tại D và tam giác ACD vuông tại D có:
AB = AC (chứng minh trên).
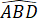 =
= 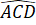 (chứng minh trên).
(chứng minh trên).
Do đó ΔABD = ΔACD (cạnh huyền – góc nhọn).
Khi đó BD = CD (2 cạnh tương ứng) hay D là trung điểm của đoạn thẳng BC.
Do AD vuông góc với BC tại trung điểm của BC nên AD là đường trung trực của đoạn thẳng BC.
Vậy đường thẳng AD là đường trung trực của đoạn thẳng BC.

Giải:
Do tam giác ABC cân tại A nên:
Xét 2 tam giác vuông BFC và CEB:
BC chung
=> ΔBFC = ΔCEB (cạnh huyền – góc nhọn)
=>BE = CF (2 cạnh tương ứng).
Bài 4.24 - Trang 84: Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
Giải:


Bài 4.25 - Trang 84: Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
Giải:
a.

Do M là trung điểm của BC nên MB = MC.
Do AM⊥BC nên tam giác AMB vuông tại M, tam giác AMC vuông tại M.
Xét hai tam giác AMB vuông tại M và AMC vuông tại M có:
AM chung.
MB = MC (chứng minh trên).
Do đó ΔAMB = ΔAMC (2 cạnh góc vuông).
Khi đó AB = AC (2 cạnh tương ứng).
Tam giác ABC có AB = AC nên tam giác ABC cân tại A.
Vậy tam giác ABC cân tại A.
b)


Bài 4.26 - Trang 84: Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân.
Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng 45°;
c) Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
Giải:
a. Dựa vào định lý tổng ba góc trong 1 tam giác bằng180° => tam giác không thể có 2 góc vuông
=>Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau
=> Tam giác vuông cân thì cân tại đỉnh góc vuông.
b. Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau => Tổng hai góc nhọn sẽ bằng : 180° - 90° = 90°
=> Mỗi góc nhọn sẽ là 45°
Vậy tam giác vuông cân có hai góc nhọn bằng 45°.
c. Áp dụng định lý tổng ba góc trong 1 tam giác bằng 180° , ta có số đo góc còn lại là : 180° - 90° - 45° = 45°
Vậy tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
Bài 4.27 - Trang 84: Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB?

Giải:
Trong Hình 4.70, ta thấy đường thẳng m vuông góc với AB tại trung điểm của AB nên đường thẳng m là đường trung trực của đoạn thẳng AB.
Bài 4.27 - Trang 84: Cho tam giác ABC cân tại A có đường cao AD. Chứng minh rằng đường thẳng AD là đường trung trực của đoạn thẳng BC.
Giải:
Do tam giác ABC cân tại A nên AB = AC,
hay
Do AD là đường cao của tam giác ABC hay AD ⊥ BC tại D nên tam giác ABD vuông tại D và tam giác ACD vuông tại D.
Xét hai tam giác ABD vuông tại D và tam giác ACD vuông tại D có:
AB = AC (chứng minh trên).
Do đó ΔABD = ΔACD (cạnh huyền – góc nhọn).
Khi đó BD = CD (2 cạnh tương ứng) hay D là trung điểm của đoạn thẳng BC.
Do AD vuông góc với BC tại trung điểm của BC nên AD là đường trung trực của đoạn thẳng BC.
Vậy đường thẳng AD là đường trung trực của đoạn thẳng BC.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025