Giải SGK Toán 7 sách Kết nối tri thức: Luyện tập chung trang 86
Giải SGK Toán 7 sách Kết nối tri thức: Luyện tập chung - Trang 86.
Bài 4.29 - Trang 86: Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.
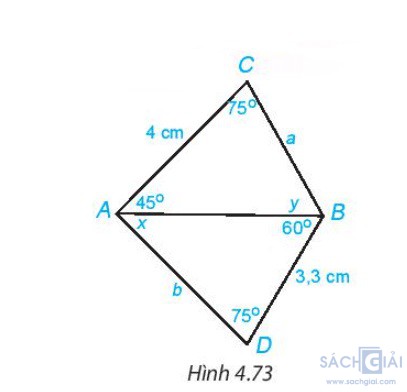
Giải:

Bài 4.30 - Trang 86: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM.
Chứng minh rằng:
a) Δ OAN = Δ OBM;
b) Δ AMN = Δ BNM.
Giải:
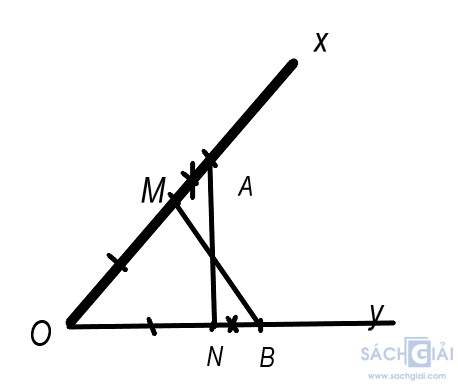
a. Xét ΔOAN và ΔOBM, ta có :
OA = OB
Góc O chung
OM = ON
=> ΔOAN = ΔOBM (c-g-c)
b. Từ câu a => AN= BM. Mà OA = OB => AM =BN
Xét ΔAMN và ΔBNM, ta có :
AN = BM
AM = BN
MN chung
=> ΔAMN = ΔBNM (c-c-c)
Bài 4.31 - Trang 86: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
a) AC = BD;
b) Δ ACD = Δ BDC.
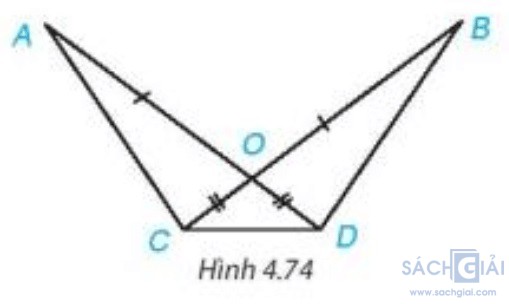
Giải:
a) Xét hai tam giác AOC và BOD có:
OA = OB (theo giả thiết).
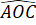 =
= 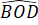 (2 góc đối đỉnh).
(2 góc đối đỉnh).
OC = OD (theo giả thiết).
Do đó ΔAOC = ΔBOD (c – g – c).
Vậy AC = BD (2 cạnh tương ứng).
b) Có AD = OA + OD, BC = OB + OC.
Mà OA = OB, OC = OD nên AD = BC.
Xét hai tam giác ACD và BDC có:
AD = BC (chứng minh trên).
AC = BD (chứng minh trên).
CD chung.
Vậy ΔACD = ΔBDC (c – c – c).
Bài 4.32 - Trang 86: Cho tam giác MBC vuông tại M có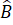 = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
= 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Giải:
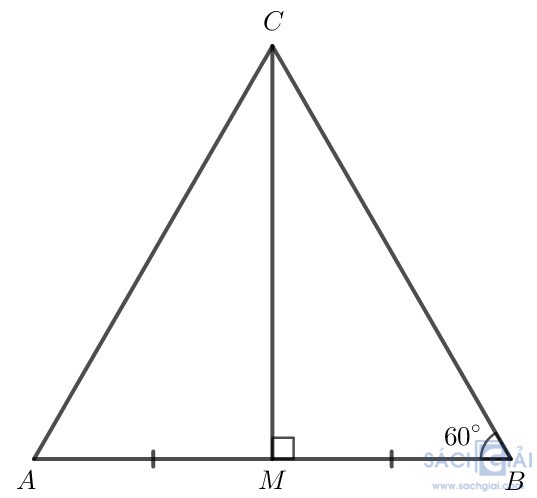
Xét hai tam giác AMC vuông tại M và BMC vuông tại M có:
AM = BM (theo giả thiết).
MC chung.
Do đó ΔAMC = ΔBMC (2 cạnh góc vuông).
Khi đó AC = BC (2 cạnh tương ứng).
Tam giác ABC có AC = BC nên tam giác ABC cân tại C.
Tam giác ABC cân tại C lại có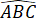 = 60o nên tam giác ABC là tam giác đều.
= 60o nên tam giác ABC là tam giác đều.
Vậy tam giác ABC là tam giác đều.

Giải:

Bài 4.30 - Trang 86: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM.
Chứng minh rằng:
a) Δ OAN = Δ OBM;
b) Δ AMN = Δ BNM.
Giải:

a. Xét ΔOAN và ΔOBM, ta có :
OA = OB
Góc O chung
OM = ON
=> ΔOAN = ΔOBM (c-g-c)
b. Từ câu a => AN= BM. Mà OA = OB => AM =BN
Xét ΔAMN và ΔBNM, ta có :
AN = BM
AM = BN
MN chung
=> ΔAMN = ΔBNM (c-c-c)
Bài 4.31 - Trang 86: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
a) AC = BD;
b) Δ ACD = Δ BDC.

Giải:
a) Xét hai tam giác AOC và BOD có:
OA = OB (theo giả thiết).
OC = OD (theo giả thiết).
Do đó ΔAOC = ΔBOD (c – g – c).
Vậy AC = BD (2 cạnh tương ứng).
b) Có AD = OA + OD, BC = OB + OC.
Mà OA = OB, OC = OD nên AD = BC.
Xét hai tam giác ACD và BDC có:
AD = BC (chứng minh trên).
AC = BD (chứng minh trên).
CD chung.
Vậy ΔACD = ΔBDC (c – c – c).
Bài 4.32 - Trang 86: Cho tam giác MBC vuông tại M có
Giải:

Xét hai tam giác AMC vuông tại M và BMC vuông tại M có:
AM = BM (theo giả thiết).
MC chung.
Do đó ΔAMC = ΔBMC (2 cạnh góc vuông).
Khi đó AC = BC (2 cạnh tương ứng).
Tam giác ABC có AC = BC nên tam giác ABC cân tại C.
Tam giác ABC cân tại C lại có
Vậy tam giác ABC là tam giác đều.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025