Giải Toán 8 sách Kết nối Tri Thức, bài 3: Phép cộng và phép trừ đa thức
Giải Toán 8 sách Kết nối Tri Thức, bài 3: Phép cộng và phép trừ đa thức - Trang 15, 16.
Hoạt động 1 trang 15: Cho hai đa thức 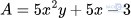 và
và 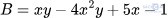
Thực hiện phép cộng hai đa thức A và B bằng cách tiến hành các bước sau:
Lập tổng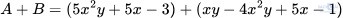
Bỏ dấu ngoặc và thu gọn đa thức nhận được
Giải:
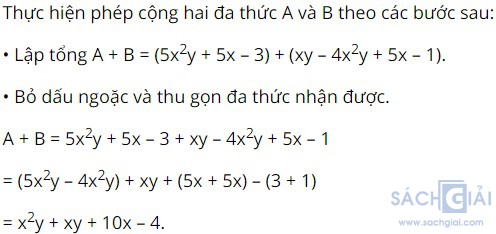
Hoạt động 2 trang 15: Cho hai đa thức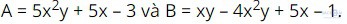
Thực hiện phép trừ hai đa thức A và B bằng cách lập hiệu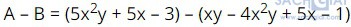 , bỏ dấu ngoặc và thu gọn đa thức nhận được
, bỏ dấu ngoặc và thu gọn đa thức nhận được
Giải:
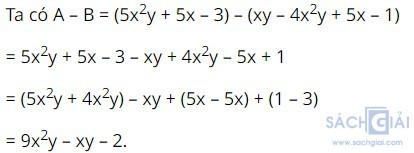
Luyện tập 1 trang 16: Cho hai đa thức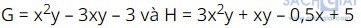 . Hãy tính G + H và G - H
. Hãy tính G + H và G - H
Giải:
Ta có:
• G + H = (x2y – 3xy – 3) + (3x2y + xy – 0,5x + 5)
= x2y – 3xy – 3 + 3x2y + xy – 0,5x + 5
= (x2y + 3x2y) + (– 3xy + xy) – 0,5x + (– 3 + 5)
= 4x2y – 2xy – 0,5x + 2.
• G – H = (x2y – 3xy – 3) – (3x2y + xy – 0,5x + 5)
= x2y – 3xy – 3 – 3x2y – xy + 0,5x – 5
= (x2y – 3x2y) + (– 3xy – xy) + 0,5x + (– 3 – 5)
= –2x2y – 4xy + 0,5x – 8.
Luyện tập 2 trang 16: Rút gọn và tính giá trị của biểu thức sau tại x = 2 và y = -1
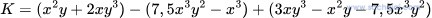
Giải:
K = (x2y + 2xy3) – (7,5x3y2 – x3) + (3xy3 – x2y + 7,5x3y2)
= x2y + 2xy3 – 7,5x3y2 + x3 + 3xy3 – x2y + 7,5x3y2
= (x2y – x2y) + (2xy3 + 3xy3) + (7,5x3y2 – 7,5x3y2) + x3
= 5xy3 + x3.
Thay x = 2 và y = −1 vào đa thức thu gọn ở trên, ta được:
K = 5.2.(–1)3 + 23 = 10.(–1) + 8 = –2.
Vận dụng trang 16: Trở lại tình huống mở đầu, hãy trình bày ý kiến của em.
Trong buổi sinh hoạt câu lạc bộ Toán học của lớp, hai bạn tính giá trị của hai đa thức P = 2x2y – xy2 + 22 và Q = xy2 – 2x2y + 23 tại những giá trị cho trước của x và y. Kết quả được ghi lại như bảng bên.
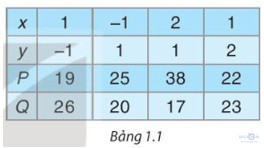
Ban giám khảo cho biết một cột chắc chắn có kết quả sai.
Theo em, làm thế nào để có thể nhanh chóng phát hiện cột đó?
Giải:
Ta có P + Q = (2x2y – xy2 + 22) + (xy2 – 2x2y + 23)
= 2x2y – xy2 + 22 + xy2 – 2x2y + 23
= (2x2y – 2x2y) + (xy2 – xy2) + 23 + 22 = 45.
Ta xét từng cột trong bảng trên, ta có:
• Cột thứ nhất: P + Q = 19 + 26 = 45;
• Cột thứ hai: P + Q = 25 + 20 = 45;
• Cột thứ ba: P + Q = 38 + 17 = 55;
• Cột thứ tư: P + Q = 22 + 23 = 45.
Vì tổng P + Q luôn bằng 45 nên cột thứ ba có kết quả sai.
Thực hiện phép cộng hai đa thức A và B bằng cách tiến hành các bước sau:
Lập tổng
Bỏ dấu ngoặc và thu gọn đa thức nhận được
Giải:
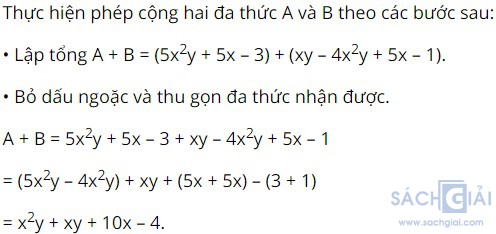
Hoạt động 2 trang 15: Cho hai đa thức
Thực hiện phép trừ hai đa thức A và B bằng cách lập hiệu
Giải:
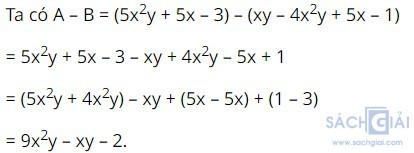
Luyện tập 1 trang 16: Cho hai đa thức
Giải:
Ta có:
• G + H = (x2y – 3xy – 3) + (3x2y + xy – 0,5x + 5)
= x2y – 3xy – 3 + 3x2y + xy – 0,5x + 5
= (x2y + 3x2y) + (– 3xy + xy) – 0,5x + (– 3 + 5)
= 4x2y – 2xy – 0,5x + 2.
• G – H = (x2y – 3xy – 3) – (3x2y + xy – 0,5x + 5)
= x2y – 3xy – 3 – 3x2y – xy + 0,5x – 5
= (x2y – 3x2y) + (– 3xy – xy) + 0,5x + (– 3 – 5)
= –2x2y – 4xy + 0,5x – 8.
Luyện tập 2 trang 16: Rút gọn và tính giá trị của biểu thức sau tại x = 2 và y = -1
Giải:
K = (x2y + 2xy3) – (7,5x3y2 – x3) + (3xy3 – x2y + 7,5x3y2)
= x2y + 2xy3 – 7,5x3y2 + x3 + 3xy3 – x2y + 7,5x3y2
= (x2y – x2y) + (2xy3 + 3xy3) + (7,5x3y2 – 7,5x3y2) + x3
= 5xy3 + x3.
Thay x = 2 và y = −1 vào đa thức thu gọn ở trên, ta được:
K = 5.2.(–1)3 + 23 = 10.(–1) + 8 = –2.
Vận dụng trang 16: Trở lại tình huống mở đầu, hãy trình bày ý kiến của em.
Trong buổi sinh hoạt câu lạc bộ Toán học của lớp, hai bạn tính giá trị của hai đa thức P = 2x2y – xy2 + 22 và Q = xy2 – 2x2y + 23 tại những giá trị cho trước của x và y. Kết quả được ghi lại như bảng bên.

Ban giám khảo cho biết một cột chắc chắn có kết quả sai.
Theo em, làm thế nào để có thể nhanh chóng phát hiện cột đó?
Giải:
Ta có P + Q = (2x2y – xy2 + 22) + (xy2 – 2x2y + 23)
= 2x2y – xy2 + 22 + xy2 – 2x2y + 23
= (2x2y – 2x2y) + (xy2 – xy2) + 23 + 22 = 45.
Ta xét từng cột trong bảng trên, ta có:
• Cột thứ nhất: P + Q = 19 + 26 = 45;
• Cột thứ hai: P + Q = 25 + 20 = 45;
• Cột thứ ba: P + Q = 38 + 17 = 55;
• Cột thứ tư: P + Q = 22 + 23 = 45.
Vì tổng P + Q luôn bằng 45 nên cột thứ ba có kết quả sai.
* GIẢI BÀI TẬP TRANG 16
Bài 1.14: Tính tổng và hiệu hai đa thức 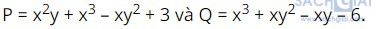
Giải:
Ta có:
• P + Q = (x2y + x3 – xy2 + 3) + (x3 + xy2 – xy – 6)
= x2y + x3 – xy2 + 3 + x3 + xy2 – xy – 6
= x2y + (x3 + x3) + (xy2 – xy2) – xy + (3 – 6)
= x2y + 2x3 – xy – 3.
• P – Q = (x2y + x3 – xY2 + 3) – (x3 + xy2 – xy – 6)
= x2y + x3 – xY2 + 3 – x3 – xY2 + xy + 6
= x2y + (x3 – x3) – (xY2 + xY2) + xy + (6 + 3)
= x2y – 2xy2 + xy + 9.
Vậy P + Q = x2y + 2x3 – xy – 3; P – Q = x2y – 2xy2 + xy + 9.
Bài 1.15: Rút gọn biểu thức:
a) (x - y) + (y - z) + (z - x)
b) (2x - 3y) + (2y - 3z) + (2z - 3x)
Giải:
a) (x - y) + (y - z) + (z - x) = x - y + y - z + z - x = 0
b) (2x - 3y) + (2y - 3z) + (2z - 3x) = 2x - 3y + 2y - 3z + 2z - 3x = - x - y - z
Bài 1.16: Tìm đa thức M biết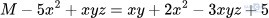
Giải:
Ta có M – 5x2 + xyz = xy + 2x2 – 3xyz + 5
Suy ra: M = xy + 2x2 – 3xyz + 5 + 5x2 – xyz
= (5x2 + 2x2) – (3xyz + xyz) + xy + 5
= 7x2 – 4xyz + xy + 5.
Vậy M = 7x2 – 4xyz + xy + 5.
Bài 1.17: Cho hai đa thức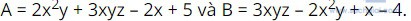
a) Tìm các đa thức A + B và A - B
b) Tính giá trị của các đa thức A và A + B tại x = 0,5; y = -2 và z = 1
Giải:
a) Ta có:
• A + B = (2x2y + 3xyz – 2x + 5) + (3xyz – 2x2y + x – 4)
= 2x2y + 3xyz – 2x + 5 + 3xyz – 2x2y + x – 4
= (2x2y – 2x2y) + (3xyz + 3xyz) + (x – 2x) + (5 – 4)
= 6xyz – x + 1.
• A – B = (2x2y + 3xyz – 2x + 5) – (3xyz – 2x2y + x – 4)
= 2x2y + 3xyz – 2x + 5 – 3xyz + 2x2y – x + 4
= (2x2y + 2x2y) + (3xyz – 3xyz) – (2x + x) + (5 + 4)
= 4x2y – 3x + 9.
Vậy A + B = 6xyz – x + 1; A – B = 4x2y – 3x + 9.
b) Thay x = 0,5; y = −2 và z = 1 vào biểu thức A, ta được:
A = 2 . 0,52 . (−2) + 3 . 0,5 . (−2) . 1 – 2 . 0,5 + 5
= 2 . 0,25 . (−2) + 1,5 . (−2) – 1 + 5
= 0,5 . (−2) – 3 + 4 = −1 – 3 + 4 = 0.
Thay x = 0,5; y = −2 và z = 1 vào biểu thức A + B, ta được:
A + B = 6 . 0,5 . (−2) . 1 – 0,5 + 1
= 3 . (−2) – 0,5 + 1 = −6 + 0,5 = −5,5.
Vậy tại x = 0,5; y = −2 và z = 1 thì A = 0 và A + B = −5,5.
Giải:
Ta có:
• P + Q = (x2y + x3 – xy2 + 3) + (x3 + xy2 – xy – 6)
= x2y + x3 – xy2 + 3 + x3 + xy2 – xy – 6
= x2y + (x3 + x3) + (xy2 – xy2) – xy + (3 – 6)
= x2y + 2x3 – xy – 3.
• P – Q = (x2y + x3 – xY2 + 3) – (x3 + xy2 – xy – 6)
= x2y + x3 – xY2 + 3 – x3 – xY2 + xy + 6
= x2y + (x3 – x3) – (xY2 + xY2) + xy + (6 + 3)
= x2y – 2xy2 + xy + 9.
Vậy P + Q = x2y + 2x3 – xy – 3; P – Q = x2y – 2xy2 + xy + 9.
Bài 1.15: Rút gọn biểu thức:
a) (x - y) + (y - z) + (z - x)
b) (2x - 3y) + (2y - 3z) + (2z - 3x)
Giải:
a) (x - y) + (y - z) + (z - x) = x - y + y - z + z - x = 0
b) (2x - 3y) + (2y - 3z) + (2z - 3x) = 2x - 3y + 2y - 3z + 2z - 3x = - x - y - z
Bài 1.16: Tìm đa thức M biết
Giải:
Ta có M – 5x2 + xyz = xy + 2x2 – 3xyz + 5
Suy ra: M = xy + 2x2 – 3xyz + 5 + 5x2 – xyz
= (5x2 + 2x2) – (3xyz + xyz) + xy + 5
= 7x2 – 4xyz + xy + 5.
Vậy M = 7x2 – 4xyz + xy + 5.
Bài 1.17: Cho hai đa thức
a) Tìm các đa thức A + B và A - B
b) Tính giá trị của các đa thức A và A + B tại x = 0,5; y = -2 và z = 1
Giải:
a) Ta có:
• A + B = (2x2y + 3xyz – 2x + 5) + (3xyz – 2x2y + x – 4)
= 2x2y + 3xyz – 2x + 5 + 3xyz – 2x2y + x – 4
= (2x2y – 2x2y) + (3xyz + 3xyz) + (x – 2x) + (5 – 4)
= 6xyz – x + 1.
• A – B = (2x2y + 3xyz – 2x + 5) – (3xyz – 2x2y + x – 4)
= 2x2y + 3xyz – 2x + 5 – 3xyz + 2x2y – x + 4
= (2x2y + 2x2y) + (3xyz – 3xyz) – (2x + x) + (5 + 4)
= 4x2y – 3x + 9.
Vậy A + B = 6xyz – x + 1; A – B = 4x2y – 3x + 9.
b) Thay x = 0,5; y = −2 và z = 1 vào biểu thức A, ta được:
A = 2 . 0,52 . (−2) + 3 . 0,5 . (−2) . 1 – 2 . 0,5 + 5
= 2 . 0,25 . (−2) + 1,5 . (−2) – 1 + 5
= 0,5 . (−2) – 3 + 4 = −1 – 3 + 4 = 0.
Thay x = 0,5; y = −2 và z = 1 vào biểu thức A + B, ta được:
A + B = 6 . 0,5 . (−2) . 1 – 0,5 + 1
= 3 . (−2) – 0,5 + 1 = −6 + 0,5 = −5,5.
Vậy tại x = 0,5; y = −2 và z = 1 thì A = 0 và A + B = −5,5.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025