Giải Toán 8 sách Kết nối Tri Thức, bài 1: Đơn thức
Giải Toán 8 sách Kết nối Tri Thức, bài 1: Đơn thức - Trang 6, 7, ..., 10.
1. Đơn thức và đơn thức thu gọn
Hoạt động 1 - Trang 6:
Biểu thức x2- 2x có phải là đơn thức một biến không? Vì sao? Hãy cho một vài ví dụ về đơn thức một biến.
Giải:
Biểu thức x2- 2x không phải là đơn thức một biến không.
Vì đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.
Ví dụ về đơn thức một biến: 9; 2x3y; − xy2z5
Hoạt động 2 trang 6: Xét các biểu thức đại số:
Xét các biểu thức đại số:
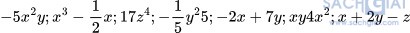
Hãy sắp xếp các biểu thức đó thành hai nhóm:
Nhóm 1: Những biểu thức có chứa phép cộng hoặc phép trừ.
Nhóm 2: Các biểu thức còn lại.
Nếu hiểu đơn thức (nhiều biến) tương tự đơn thức một biến thì theo em, nhóm nào trong hai nhóm trên bao gồm những đơn thức?
Giải:
Nhóm 1: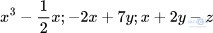
Nhóm 2: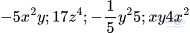
Nhóm 2 bao gồm những đơn thức vì chỉ gồm tích của số và các biến.
Luyện tập 1 trang 6: Trong các biểu thức sau đây, biểu thức nào là đơn thức?
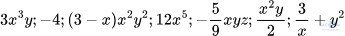
Giải:
Các biểu thức là đơn thức là: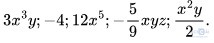
Tranh luận trang 6: Bạn Pi đặt câu hỏi: Biểu thức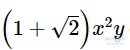 có phải là đơn thức không?
có phải là đơn thức không?
Bạn Tròn trả lời: Mình nghĩ là đúng, đó là một đơn thức.
Bạn Vuông cho rằng: Mình nghĩ không phải, bởi vì trong đó có phép cộng.
Còn em nghĩ sao?
Giải:
Vì giá trị của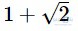 là một số thực nên biểu thức
là một số thực nên biểu thức 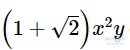 là tích của số thực với các biến.
là tích của số thực với các biến.
Do đó, biểu thức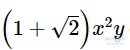 là đơn thức.
là đơn thức.
Câu hỏi trang 7 Toán 8 Tập 1: Cho biết hệ số, phần biến và bậc của mỗi đơn thức sau: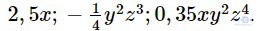
Giải:

Luyện tập 2 trang 8: Thu gọn và xác định bậc của đơn thức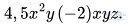
Giải:
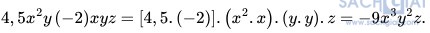
Đơn thức có bậc là: 3 + 2 + 1 = 6.
Biểu thức x2- 2x có phải là đơn thức một biến không? Vì sao? Hãy cho một vài ví dụ về đơn thức một biến.
Giải:
Biểu thức x2- 2x không phải là đơn thức một biến không.
Vì đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.
Ví dụ về đơn thức một biến: 9; 2x3y; − xy2z5
Hoạt động 2 trang 6: Xét các biểu thức đại số:
Xét các biểu thức đại số:
Hãy sắp xếp các biểu thức đó thành hai nhóm:
Nhóm 1: Những biểu thức có chứa phép cộng hoặc phép trừ.
Nhóm 2: Các biểu thức còn lại.
Nếu hiểu đơn thức (nhiều biến) tương tự đơn thức một biến thì theo em, nhóm nào trong hai nhóm trên bao gồm những đơn thức?
Giải:
Nhóm 1:
Nhóm 2:
Nhóm 2 bao gồm những đơn thức vì chỉ gồm tích của số và các biến.
Luyện tập 1 trang 6: Trong các biểu thức sau đây, biểu thức nào là đơn thức?
Giải:
Các biểu thức là đơn thức là:
Tranh luận trang 6: Bạn Pi đặt câu hỏi: Biểu thức
Bạn Tròn trả lời: Mình nghĩ là đúng, đó là một đơn thức.
Bạn Vuông cho rằng: Mình nghĩ không phải, bởi vì trong đó có phép cộng.
Còn em nghĩ sao?
Giải:
Vì giá trị của
Do đó, biểu thức
Câu hỏi trang 7 Toán 8 Tập 1: Cho biết hệ số, phần biến và bậc của mỗi đơn thức sau:
Giải:

Luyện tập 2 trang 8: Thu gọn và xác định bậc của đơn thức
Giải:
Đơn thức có bậc là: 3 + 2 + 1 = 6.
2. Đơn thức đồng dạng
Hoạt động 3 trang 8: Cho đơn thức một biến M = 3x2. Hãy viết ba đơn thức biến x, cùng bậc với M rồi so sánh phần biến của các đơn thức đó
Giải:
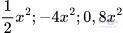
Phần biến của các đơn thức giống nhau
Phần biến của các đơn thức giống nhau
Hoạt động 4 trang 8: Xét ba đơn thức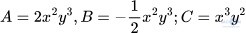
a) Bậc của ba đơn thức A, B và C
b) Phần biến của ba đơn thức A, B và C
Giải:
a) Cả ba đơn thức đều có bậc là 5
b) Phần biến của đơn thức A giống đơn thức B và khác đơn thức C
Luyện tập 3 trang 8: Cho các đơn thức: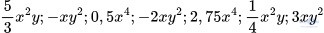
Hãy sắp xếp các đơn thức đã cho thành từng nhóm, sao cho tất cả các đơn thức đồng dạng thì cùng một nhóm.
Giải:
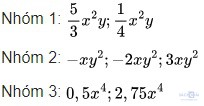
Tranh luận trang 8: Ta đã biết nếu hai đơn thức một biến có cùng biến và có cùng bậc thì đồng dạng với nhau. Hỏi điều đó còn đúng không đối với hai đơn thức hai biến (nhiều hơn một biến)?
Giải:
Hai đơn thức một biến có cùng biến và có cùng bậc thì đồng dạng với nhau. Điều này không đúng với hai đơn thức hai biến (nhiều hơn một biến).
Chẳng hạn: Trong Hoạt động 4, cả ba đơn thức A, B và C đều có cùng biến x, y và có cùng bậc nhưng chỉ có đơn thức A và B là đồng dạng do có cùng phần biến x2y3.
Đơn thức C có phần biến x3y2 khác x2y3 nên không đồng dạng với hai đơn thức A, B.
Hoạt động 5 trang 8: Quan sát ví dụ sau:
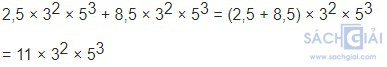
Trong ví dụ này, ta đã vận dụng tính chất gì của phép nhân để thu gọn tổng ban đầu?
Giải:
Trong ví dụ này, ta đã vận dụng tính chất phân phối của phép nhân đối với phép cộng để thu gọn tổng ban đầu.
Hoạt động 6 trang 8: Cho hai đơn thức đồng dạng M = 2,5x2y3 và P = 8,5x2y3. Tương tự HĐ5, hãy:
a) Thu gọn tổng M + P
b) Thu gọn hiệu M - P
Giải:
a) M + P = 2,5x2y3 + 8,5x2y3
= (2,5 + 8,5)x2y3 = 11x2y3
b) M − P = 2,5x2y3 − 8,5x2y3
= (2,5 − 8,5)x2y3 = − 6x2y3
Luyện tập 4 trang 9: Cho các đơn thức − x3y; 4x3y và − 2x3y
a) Tính tổng S của ba đơn thức đó.
b) Tính giá trị tổng S tại x = 2; y = -3
Giải:
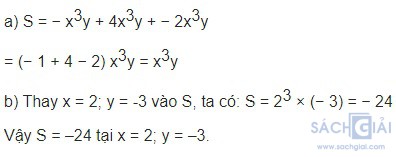
Giải:
Phần biến của các đơn thức giống nhau
Phần biến của các đơn thức giống nhau
Hoạt động 4 trang 8: Xét ba đơn thức
a) Bậc của ba đơn thức A, B và C
b) Phần biến của ba đơn thức A, B và C
Giải:
a) Cả ba đơn thức đều có bậc là 5
b) Phần biến của đơn thức A giống đơn thức B và khác đơn thức C
Luyện tập 3 trang 8: Cho các đơn thức:
Hãy sắp xếp các đơn thức đã cho thành từng nhóm, sao cho tất cả các đơn thức đồng dạng thì cùng một nhóm.
Giải:
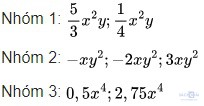
Tranh luận trang 8: Ta đã biết nếu hai đơn thức một biến có cùng biến và có cùng bậc thì đồng dạng với nhau. Hỏi điều đó còn đúng không đối với hai đơn thức hai biến (nhiều hơn một biến)?
Giải:
Hai đơn thức một biến có cùng biến và có cùng bậc thì đồng dạng với nhau. Điều này không đúng với hai đơn thức hai biến (nhiều hơn một biến).
Chẳng hạn: Trong Hoạt động 4, cả ba đơn thức A, B và C đều có cùng biến x, y và có cùng bậc nhưng chỉ có đơn thức A và B là đồng dạng do có cùng phần biến x2y3.
Đơn thức C có phần biến x3y2 khác x2y3 nên không đồng dạng với hai đơn thức A, B.
Hoạt động 5 trang 8: Quan sát ví dụ sau:
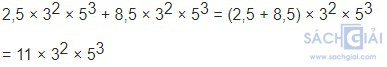
Trong ví dụ này, ta đã vận dụng tính chất gì của phép nhân để thu gọn tổng ban đầu?
Giải:
Trong ví dụ này, ta đã vận dụng tính chất phân phối của phép nhân đối với phép cộng để thu gọn tổng ban đầu.
Hoạt động 6 trang 8: Cho hai đơn thức đồng dạng M = 2,5x2y3 và P = 8,5x2y3. Tương tự HĐ5, hãy:
a) Thu gọn tổng M + P
b) Thu gọn hiệu M - P
Giải:
a) M + P = 2,5x2y3 + 8,5x2y3
= (2,5 + 8,5)x2y3 = 11x2y3
b) M − P = 2,5x2y3 − 8,5x2y3
= (2,5 − 8,5)x2y3 = − 6x2y3
Luyện tập 4 trang 9: Cho các đơn thức − x3y; 4x3y và − 2x3y
a) Tính tổng S của ba đơn thức đó.
b) Tính giá trị tổng S tại x = 2; y = -3
Giải:
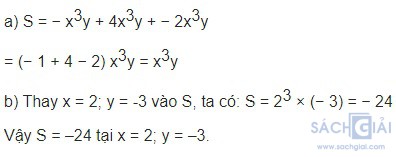
3. Giải bài tập trang 9, 10
Bài 1.1: Trong các biểu thức sau, biểu thức nào là đơn thức?
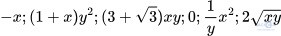
Giải:
Các biểu thức là đơn thức gồm:
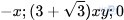
Bài 1.2: Cho các đơn thức:
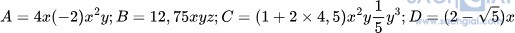
a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.
b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.
Giải:
a) Các đơn thức đã thu gọn: B, D
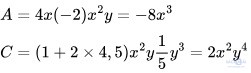
b) Hệ số của đơn thức A là -8, phần biến là x3y và bậc là 4
Hệ số của đơn thức B là 12,75, phần biến xyz là và bậc là 3
Hệ số của đơn thức C là 2, phần biến là x2y4 và bậc là 6
Hệ số của đơn thức A là phần 2 -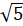 biến là x và bậc là 1
biến là x và bậc là 1
Bài 1.3: Thu gọn rồi tính giá trị của mỗi đơn thức sau:
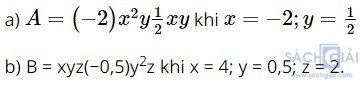
Giải:

Bài 1.4: Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau:
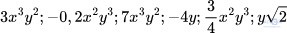
Giải:
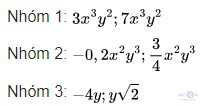
Bài tập 1.5: Rút gọn rồi tính giá trị của biểu thức
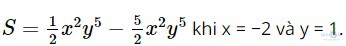
Giải:
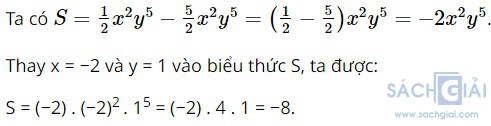
Bài 1.6: Tính tổng của bốn đơn thức:
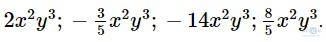
Giải:
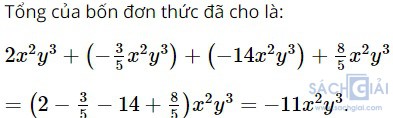
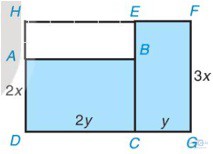
Bài 1.7: Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến x và y biểu thị diện tích của mảnh đất đã cho bằng hai cách:
Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC
Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA
Giải:
Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC.
Diện tích hình chữ nhật ABCD là: 2x . 2y = 4xy (đvdt);
Diện tích hình chữ nhật EFGC là: 3x . y = 3xy (đvdt);
Diện tích mảnh đất tô màu xanh là: 4xy + 3xy = 7xy (đvdt).
Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA.
Diện tích hình chữ nhật HFGD là: 3x(2y + y) = 3x . 3y = 9xy (đvdt);
Diện tích hình chữ nhật HEBA là: (3x – 2x) . 2y = x . 2y = 2xy (đvdt);
Diện tích mảnh đất tô màu xanh là: 9xy – 2xy = 7xy (đvdt).
Giải:
Các biểu thức là đơn thức gồm:
Bài 1.2: Cho các đơn thức:
a) Liệt kê các đơn thức thu gọn trong các đơn thức đã cho và thu gọn các đơn thức còn lại.
b) Với mỗi đơn thức nhận được, hãy cho biết hệ số, phần biến và bậc của nó.
Giải:
a) Các đơn thức đã thu gọn: B, D
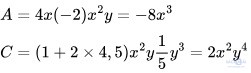
b) Hệ số của đơn thức A là -8, phần biến là x3y và bậc là 4
Hệ số của đơn thức B là 12,75, phần biến xyz là và bậc là 3
Hệ số của đơn thức C là 2, phần biến là x2y4 và bậc là 6
Hệ số của đơn thức A là phần 2 -
Bài 1.3: Thu gọn rồi tính giá trị của mỗi đơn thức sau:
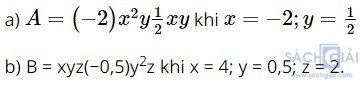
Giải:

Bài 1.4: Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau:
Giải:
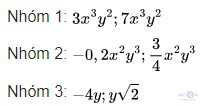
Bài tập 1.5: Rút gọn rồi tính giá trị của biểu thức
Giải:
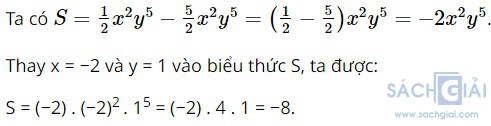
Bài 1.6: Tính tổng của bốn đơn thức:
Giải:
Bài 1.7: Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến x và y biểu thị diện tích của mảnh đất đã cho bằng hai cách:
Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC
Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA

Giải:
Cách 1. Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC.
Diện tích hình chữ nhật ABCD là: 2x . 2y = 4xy (đvdt);
Diện tích hình chữ nhật EFGC là: 3x . y = 3xy (đvdt);
Diện tích mảnh đất tô màu xanh là: 4xy + 3xy = 7xy (đvdt).
Cách 2. Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA.
Diện tích hình chữ nhật HFGD là: 3x(2y + y) = 3x . 3y = 9xy (đvdt);
Diện tích hình chữ nhật HEBA là: (3x – 2x) . 2y = x . 2y = 2xy (đvdt);
Diện tích mảnh đất tô màu xanh là: 9xy – 2xy = 7xy (đvdt).
Ý kiến bạn đọc
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025