Giải Toán 8 sách Kết nối Tri Thức, bài: Luyện tập chung trang 17
Giải Toán 8 sách Kết nối Tri Thức, bài: Luyện tập chung - Trang 17.
Bài 1.18: Cho các biểu thức:
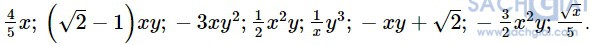
a) Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?
b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.
c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.
Giải:


Bài 1.19: Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là 1,2 m, đáy hình hộp chữ nhật có chiều dài x mét, chiều rộng y mét. Bể thứ hai có chiều sâu là 1,5 m, hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ nhất.
a) Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.
b) Tính lượng nước bơm đầy hai bể nếu x = 4m, y = 3m
Giải:
a) Bể thứ hai có đáy là hình chữ nhật có chiều dài 5x mét và chiều rộng là 5y mét.
Số mét khối nước cần có để bơm đầy cả hai bể bơi là thể tích nước chứa được ở hai bể bơi.
Biểu thức biểu thị số mét khối nước cần có để bơm đầy bể thứ nhất là: 1,2xy (m3).
Biểu thức biểu thị số mét khối nước cần có để bơm đầy bể thứ hai là:
1,5 . 5x . 5y = 37,5xy (m3).
Do đó, biểu thức biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi là:
1,2xy + 37,5xy = 38,7xy (m3).
b) Khi x = 5 m, y = 3 m, lượng nước cần có để bơm đầy hai bể là”
V = 38,7 . 5 . 3 = 580,5 (m3).
Bài 1.20: Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x = 1; y = -2
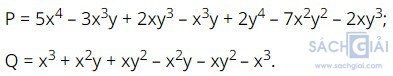
Giải:
Ta có P = 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 7x2y2 – 2xy3
= 5x4 – (3x3y + x3y) + (2xy3 – 2xy3) + 2y4 – 7x2y2
= 5x4 – 4x3y + 2y4 – 7x2y2.
Đa thức P có bậc là 4.
Thay x = 1; y = −2 vào biểu thức P, ta được:
P = 5 . 14 – 4 . 13 . (−2) + 2. (−2)4 – 7 . 12 . (−2)2
= 5 – 4 . (−2) + 2 . 16 – 7 . 4
= 5 + 8 + 32 – 28 = 13 + 4 = 17.
• Ta có Q = x3 + x2y + xy2 – x2y – xy2 – x3
= (x3 – x3) + (x2y – x2y) + (xy2 – xy2) = 0.
Đa thức Q là đa thức không nên không có bậc.
Bài 1.21: Cho hai đa thức:
A = 7xyz2 – 5xy2z + 3x2yz – xyz + 1; B = 7x2yz – 5xy2z + 3xyz2 – 2.
a) Tìm đa thức C sao cho A – C = B;
b) Tìm đa thức D sao cho A + D = B;
c) Tìm đa thức E sao cho E – A = B.
Giải:
a) Ta có A – C = B
Suy ra C = A – B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) – (7x2yz – 5xy2z + 3xyz2 – 2)
= 7xyz2 – 5xy2z + 3x2yz – xyz + 1 – 7x2yz + 5xy2z – 3xyz2 + 2
= (7xyz2 – 3xyz2) + (5xy2z – 5xy2z) + (3x2yz – 7x2yz) – xyz + (1 + 2)
= 4xyz2 – 4x2yz – xyz + 3.
Vậy C = 4xyz2 – 4x2yz – xyz + 3.
b) Ta có A + D = B
Suy ra D = B – A = –(A – B) = –(4xyz2 – 4x2yz – xyz + 3)
= – 4xyz2 + 4x2yz + xyz – 3.
Vậy D = – 4xyz2 + 4x2yz + xyz – 3.
c) Ta có E – A = B.
Suy ra E = A + B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) + (7x2yz – 5xy2z + 3xyz2 – 2)
= 7xyz2 – 5xy2z + 3x2yz – xyz + 1 + 7x2yz – 5xy2z + 3xyz2 – 2
= (7xyz2 + 3xyz2) – (5xy2z + 5xy2z) + (7x2yz + 3x2yz) – xyz + (1 – 2)
= 10x2yz – 10xy2z + 10xyz2 – xyz – 1.
Vậy E = 10x2yz – 10xy2z + 10xyz2 – xyz – 1.
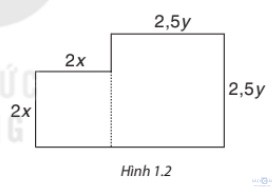
Bài 1.22: Từ một nửa miếng bìa, người ta cắt ra hai hình tròn có bán kính x cm và y xm. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu miếng bìa có hình dạng gồm hai hình vuông ghéo lại và có kích thước (cm) như hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?
Giải:
Trong Hình 1.2 có:
• Diện tích hình vuông nhỏ là: (2x)2 = 4x2 (cm2).
Diện tích hình vuông lớn là: (2,5y)2 = 6,25y2 (cm2).
Tổng diện tích hai hình vuông là: 4x2 + 6,25y2 (cm2).
• Hình tròn nhỏ có bán kính là x (cm)
Diện tích hình tròn nhỏ là: πx2 (cm2).
• Hình tròn lớn có bán kính là y (cm)
Diện tích hình tròn lớn là: πy2 (cm2).
Do đó, biểu thức biểu thị diện tích phần còn lại của miếng bìa là:
(4x2 + 6,25y2) – (πx2 + πy2)
= 4x2 + 6,25y2 – πx2 – πy2
= (4x2 – πx2) + (6,25y2 – πy2)
= (4 – π)x2 + (6,25 – π)y2
Biểu thức (4 – π)x2 + (6,25 – π)y2 là một đa thức bậc 2.
Bài 1.23: Cho ba đa thức:M = 3x3 – 4x2y + 3x – y; N = 5xy – 3x + 2; P = 3x3 + 2x2y + 7x – 1.
Tính M + N – P và M – N – P.
Giải:
Ta có:
• M + N – P = (3x3 – 4x2y + 3x – y) + (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)
= 3x3 – 4x2y + 3x – y + 5xy – 3x + 2 – 3x3 – 2x2y – 7x + 1
= (3x3 – 3x3) – (4x2y + 2x2y) + 5xy + (3x – 3x – 7x) – y + (2 + 1)
= – 6x2y + 5xy – 7x – y + 3.
• M – N – P = (3x3 – 4x2y + 3x – y) – (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)
= 3x3 – 4x2y + 3x – y – 5xy + 3x – 2 – 3x3 – 2x2y – 7x + 1
= (3x3 – 3x3) – (4x2y + 2x2y) – 5xy + (3x + 3x – 7x) – y + (1 – 2)
= – 6x2y – 5xy – x – y – 1.
Vậy M + N – P = – 6x2y + 5xy – 7x – y + 3; M – N – P = – 6x2y – 5xy – x – y – 1
a) Trong các biểu thức đã cho, biểu thức nào là đơn thức? Biểu thức nào không là đơn thức?
b) Hãy chỉ ra hệ số và phần biến của mỗi đơn thức đã cho.
c) Viết tổng tất cả các đơn thức trên để được một đa thức. Xác định bậc của đa thức đó.
Giải:


Bài 1.19: Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là 1,2 m, đáy hình hộp chữ nhật có chiều dài x mét, chiều rộng y mét. Bể thứ hai có chiều sâu là 1,5 m, hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ nhất.
a) Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.
b) Tính lượng nước bơm đầy hai bể nếu x = 4m, y = 3m
Giải:
a) Bể thứ hai có đáy là hình chữ nhật có chiều dài 5x mét và chiều rộng là 5y mét.
Số mét khối nước cần có để bơm đầy cả hai bể bơi là thể tích nước chứa được ở hai bể bơi.
Biểu thức biểu thị số mét khối nước cần có để bơm đầy bể thứ nhất là: 1,2xy (m3).
Biểu thức biểu thị số mét khối nước cần có để bơm đầy bể thứ hai là:
1,5 . 5x . 5y = 37,5xy (m3).
Do đó, biểu thức biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi là:
1,2xy + 37,5xy = 38,7xy (m3).
b) Khi x = 5 m, y = 3 m, lượng nước cần có để bơm đầy hai bể là”
V = 38,7 . 5 . 3 = 580,5 (m3).
Bài 1.20: Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x = 1; y = -2
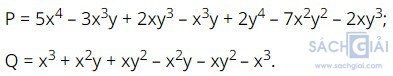
Giải:
Ta có P = 5x4 – 3x3y + 2xy3 – x3y + 2y4 – 7x2y2 – 2xy3
= 5x4 – (3x3y + x3y) + (2xy3 – 2xy3) + 2y4 – 7x2y2
= 5x4 – 4x3y + 2y4 – 7x2y2.
Đa thức P có bậc là 4.
Thay x = 1; y = −2 vào biểu thức P, ta được:
P = 5 . 14 – 4 . 13 . (−2) + 2. (−2)4 – 7 . 12 . (−2)2
= 5 – 4 . (−2) + 2 . 16 – 7 . 4
= 5 + 8 + 32 – 28 = 13 + 4 = 17.
• Ta có Q = x3 + x2y + xy2 – x2y – xy2 – x3
= (x3 – x3) + (x2y – x2y) + (xy2 – xy2) = 0.
Đa thức Q là đa thức không nên không có bậc.
Bài 1.21: Cho hai đa thức:
A = 7xyz2 – 5xy2z + 3x2yz – xyz + 1; B = 7x2yz – 5xy2z + 3xyz2 – 2.
a) Tìm đa thức C sao cho A – C = B;
b) Tìm đa thức D sao cho A + D = B;
c) Tìm đa thức E sao cho E – A = B.
Giải:
a) Ta có A – C = B
Suy ra C = A – B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) – (7x2yz – 5xy2z + 3xyz2 – 2)
= 7xyz2 – 5xy2z + 3x2yz – xyz + 1 – 7x2yz + 5xy2z – 3xyz2 + 2
= (7xyz2 – 3xyz2) + (5xy2z – 5xy2z) + (3x2yz – 7x2yz) – xyz + (1 + 2)
= 4xyz2 – 4x2yz – xyz + 3.
Vậy C = 4xyz2 – 4x2yz – xyz + 3.
b) Ta có A + D = B
Suy ra D = B – A = –(A – B) = –(4xyz2 – 4x2yz – xyz + 3)
= – 4xyz2 + 4x2yz + xyz – 3.
Vậy D = – 4xyz2 + 4x2yz + xyz – 3.
c) Ta có E – A = B.
Suy ra E = A + B = (7xyz2 – 5xy2z + 3x2yz – xyz + 1) + (7x2yz – 5xy2z + 3xyz2 – 2)
= 7xyz2 – 5xy2z + 3x2yz – xyz + 1 + 7x2yz – 5xy2z + 3xyz2 – 2
= (7xyz2 + 3xyz2) – (5xy2z + 5xy2z) + (7x2yz + 3x2yz) – xyz + (1 – 2)
= 10x2yz – 10xy2z + 10xyz2 – xyz – 1.
Vậy E = 10x2yz – 10xy2z + 10xyz2 – xyz – 1.
Bài 1.22: Từ một nửa miếng bìa, người ta cắt ra hai hình tròn có bán kính x cm và y xm. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu miếng bìa có hình dạng gồm hai hình vuông ghéo lại và có kích thước (cm) như hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?

Giải:
Trong Hình 1.2 có:
• Diện tích hình vuông nhỏ là: (2x)2 = 4x2 (cm2).
Diện tích hình vuông lớn là: (2,5y)2 = 6,25y2 (cm2).
Tổng diện tích hai hình vuông là: 4x2 + 6,25y2 (cm2).
• Hình tròn nhỏ có bán kính là x (cm)
Diện tích hình tròn nhỏ là: πx2 (cm2).
• Hình tròn lớn có bán kính là y (cm)
Diện tích hình tròn lớn là: πy2 (cm2).
Do đó, biểu thức biểu thị diện tích phần còn lại của miếng bìa là:
(4x2 + 6,25y2) – (πx2 + πy2)
= 4x2 + 6,25y2 – πx2 – πy2
= (4x2 – πx2) + (6,25y2 – πy2)
= (4 – π)x2 + (6,25 – π)y2
Biểu thức (4 – π)x2 + (6,25 – π)y2 là một đa thức bậc 2.
Bài 1.23: Cho ba đa thức:M = 3x3 – 4x2y + 3x – y; N = 5xy – 3x + 2; P = 3x3 + 2x2y + 7x – 1.
Tính M + N – P và M – N – P.
Giải:
Ta có:
• M + N – P = (3x3 – 4x2y + 3x – y) + (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)
= 3x3 – 4x2y + 3x – y + 5xy – 3x + 2 – 3x3 – 2x2y – 7x + 1
= (3x3 – 3x3) – (4x2y + 2x2y) + 5xy + (3x – 3x – 7x) – y + (2 + 1)
= – 6x2y + 5xy – 7x – y + 3.
• M – N – P = (3x3 – 4x2y + 3x – y) – (5xy – 3x + 2) – (3x3 + 2x2y + 7x – 1)
= 3x3 – 4x2y + 3x – y – 5xy + 3x – 2 – 3x3 – 2x2y – 7x + 1
= (3x3 – 3x3) – (4x2y + 2x2y) – 5xy + (3x + 3x – 7x) – y + (1 – 2)
= – 6x2y – 5xy – x – y – 1.
Vậy M + N – P = – 6x2y + 5xy – 7x – y + 3; M – N – P = – 6x2y – 5xy – x – y – 1
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025