Giải Toán 8 sách Kết nối Tri Thức: Bài tập cuối chương 3
Giải Toán 8 sách Kết nối Tri Thức: Bài tập cuối chương 3 - Trang 74, 75.
A. Trắc nghiệm
Bài 3.39: Trong các khẳng định sau, khẳng định nào đúng?
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì còn lại là góc tù
C. Nếu tứ giác có hai góc tù thì hai góc còn lại phải nhọn
D. Không có tứ giác nào có ba góc tù.
Giải:
Đáp án: B
Bài 3.40: Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành
b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành
c) Tứ giác có ba góc vuông là hình chữ nhật
d) Tứ giác có ba cạnh bằng nhau là hình thoi.
Giải:
a) b) c) Sai
c) Đúng
Bài 3.41: Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật
b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành
c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân
d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành
Giải:
a) b) c) Đúng
d) Sai
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì còn lại là góc tù
C. Nếu tứ giác có hai góc tù thì hai góc còn lại phải nhọn
D. Không có tứ giác nào có ba góc tù.
Giải:
Đáp án: B
Bài 3.40: Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành
b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành
c) Tứ giác có ba góc vuông là hình chữ nhật
d) Tứ giác có ba cạnh bằng nhau là hình thoi.
Giải:
a) b) c) Sai
c) Đúng
Bài 3.41: Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối nào cũng bằng nhau là hình chữ nhật
b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành
c) Tứ giác có hai cạnh song song và hai đường chéo bằng nhau là hình thang cân
d) Tứ giác có hai cạnh song song và hai cạnh còn lại bằng nhau là hình bình hành
Giải:
a) b) c) Đúng
d) Sai
B. Tự luận
Bài 3.42: Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.
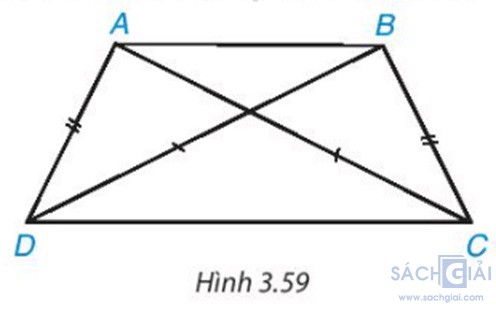
Giải:
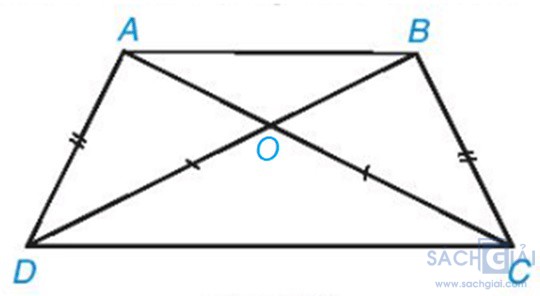
Gọi O là giao điểm của AC và BD.
Xét ∆ABC và ∆BAD có:
BC = AD (giả thiết)
AC = BD (giả thiết)
Cạnh AB chung
Do đó ∆ABC = ∆BAD (c.c.c)
Suy ra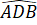 =
= 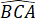 (hai góc tương ứng).
(hai góc tương ứng).
Xét ∆ACD và ∆BDC có:
AD = BC (giả thiết)
AC = BD (giả thiết)
Cạnh CD chung
Do đó ∆ADC = ∆BCD (c.c.c)
Suy ra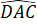 =
= 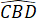 (hai góc tương ứng).
(hai góc tương ứng).
Xét ∆OAD và ∆OBC có:
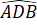 =
= 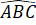 (chứng minh trên)
(chứng minh trên)
AD = BC (giả thiết)
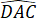 =
= 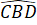 (chứng minh trên)
(chứng minh trên)
Do đó ∆OAD = ∆OBC (g.c.g).
Suy ra OA = OB; OC = OD (các cặp cạnh tương ứng).
Khi đó các tam giác OAB, OCD là tam giác cân tại O.
Suy ra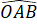 =
= 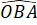 ;
; 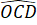 =
= 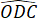
Xét ∆OAB và ∆OCD cân tại O có:
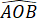 =
= 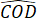 (hai góc đối đỉnh)
(hai góc đối đỉnh)
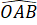 =
= 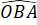 ;
; 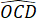 =
= 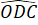
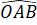 +
+ 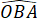 +
+ 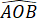 =
= 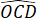 +
+ 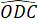 +
+ 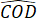 = 180o
= 180o
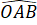 +
+ 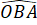 =
= 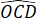 +
+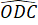
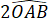 =
= 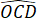
Suy ra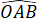 =
= 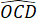 mà hai góc này ở vị trí so le trong.
mà hai góc này ở vị trí so le trong.
Do đó AB // CD.
Tứ giác ABCD có AB // CD nên ABCD là hình thang.
Hình thang ABCD có hai đường chéo AC = BD.
Do đó tứ giác ABCD là hình thang cân.
Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.
Bài 3.43: Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2 AB.
a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?
b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.
Giải:
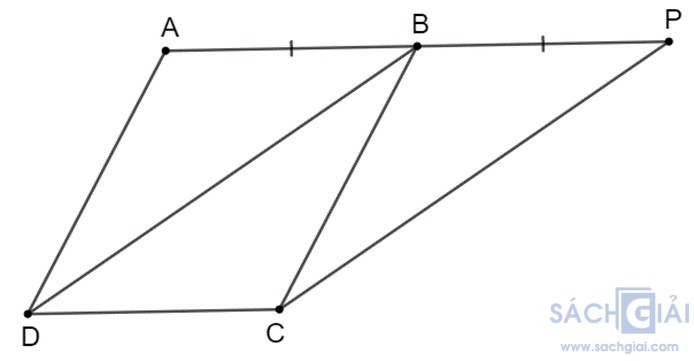
Ta có AP = 2AB suy ra AB = BP =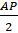
Vì ABCD là hình bình hành nên:
• AB // CD hay BP // CD
• AB = CD mà AB = BP nên BP = CD.
Tứ giác BPCD có BP // CD; BP = CD
Do đó tứ giác BPCD là hình bình hành.
b) Khi tam giác ABD vuông cân tại A thì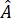 = 90o;
= 90o; 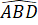 =
= 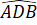 = 45o
= 45o
Ta có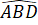 +
+ 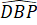 = 180o (hai góc kề bù).
= 180o (hai góc kề bù).
Suy ra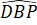 = 180o -
= 180o - 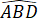 = 180o – 45o = 135o
= 180o – 45o = 135o
Do đó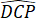 =
= 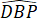 = 135o
= 135o
Vì tứ giác BPCD là hình bình hành nên BD // CP.
Suy ra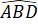 = P
= P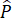 (hai góc đồng vị).
(hai góc đồng vị).
Khi đó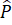 = 45o mà
= 45o mà 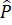 =
= 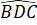 (vì tứ giác BPCD là hình bình hành).
(vì tứ giác BPCD là hình bình hành).
Do đó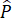 =
= 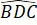 = 45o
= 45o
Vậy khi tam giác ABD vuông cân tại A thì số đo các góc của tứ giác BPCD là:
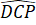 =
= 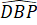 = 135o;
= 135o; 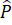 =
= 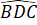 = 45o
= 45o
Bài 3.44: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.59)
a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau
b) Chứng minh tứ giác APMN là một hình chữ nhật. Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC
c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh rằng tứ giác AMCQ là một hình thoi
d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?
Giải:
a) Theo đề bài, AC ⊥ MP; AC ⊥ AB.
Suy ra MP // AB nên MP // BN.
Do đó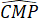 =
= 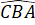 (hai góc đồng vị).
(hai góc đồng vị).
Ta có P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB
Nên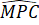 =
= 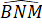 = 90o
= 90o
Xét ∆CMP và ∆MBN có:
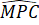 =
= 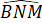 = 90o
= 90o
BM = CM (vì M là trung điểm của BC)
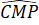 =
= 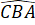 (chứng minh trên)
(chứng minh trên)
Do đó ∆CMP = ∆MBN (g.c.g).
b) Ta có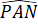 +
+ 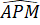 +
+ 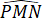 +
+ 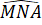 = 360o
= 360o
90o + 90o +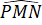 + 90o = 360o
+ 90o = 360o
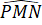 + 270o = 360o
+ 270o = 360o
Suy ra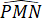 = 360o – 270o = 90o
= 360o – 270o = 90o
Tứ giác APMN có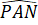 =
= 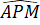 =
= 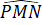 =
= 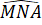 = 90o
= 90o
Do đó, tứ giác APMN là một hình chữ nhật.
Suy ra MP = AN; AP = MN (các cặp cạnh tương ứng).
Mà MP = BN; CP = MN (vì ∆CMP = ∆MBN).
Do đó AP = CP; AN = BN.
Từ đó ta suy ra N là trung điểm của AB, P là trung điểm của AC.
c) Tứ giác AMCQ có:
MP = PQ (vì P là trung điểm của MQ)
AP = CP (vì P là trung điểm của AC)
Khi đó, tứ giác AMCQ có hai đường chéo AC và MQ cắt nhau tại trung điểm P của mỗi đường nên nó là hình bình hành.
Mà MQ ⊥ AC.
Do đó tứ giác AMCQ là một hình thoi.
d) Tứ giác APMN là một hình chữ nhật nên MP = AN.
Mà P là trung điểm MQ; N là trung điểm của AB.
Suy ra MQ = AB.
Lại có AB = AC (giả thiết) nên MQ = AC.
Tứ giác AMCQ có hai đường chéo AC và MQ bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm P của mỗi đường.
Do đó, tứ giác AMCQ có là hình vuông.
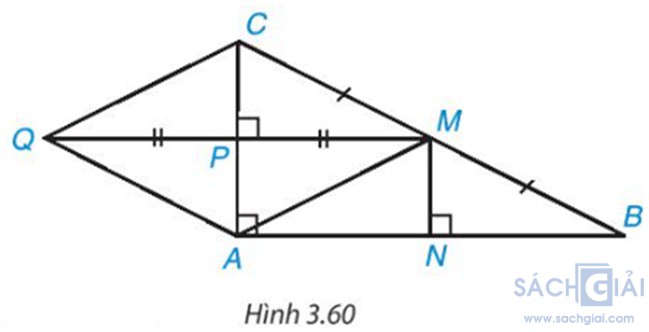
Bài 3.45: Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N là chân đường vuông góc hạ từ B xuống ME (H.3.60)
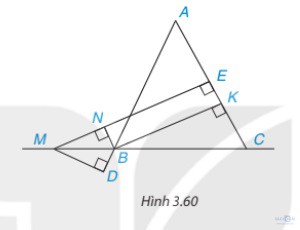
Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật
b) BK và NE cùng bằng hiệu khoảng cách từ M đến AC và AB (dù M thay đổi trên đường thẳng MC miễn là B nằm giữa M và C)
Giải:


Giải:

Gọi O là giao điểm của AC và BD.
Xét ∆ABC và ∆BAD có:
BC = AD (giả thiết)
AC = BD (giả thiết)
Cạnh AB chung
Do đó ∆ABC = ∆BAD (c.c.c)
Suy ra
Xét ∆ACD và ∆BDC có:
AD = BC (giả thiết)
AC = BD (giả thiết)
Cạnh CD chung
Do đó ∆ADC = ∆BCD (c.c.c)
Suy ra
Xét ∆OAD và ∆OBC có:
AD = BC (giả thiết)
Do đó ∆OAD = ∆OBC (g.c.g).
Suy ra OA = OB; OC = OD (các cặp cạnh tương ứng).
Khi đó các tam giác OAB, OCD là tam giác cân tại O.
Suy ra
Xét ∆OAB và ∆OCD cân tại O có:
Suy ra
Do đó AB // CD.
Tứ giác ABCD có AB // CD nên ABCD là hình thang.
Hình thang ABCD có hai đường chéo AC = BD.
Do đó tứ giác ABCD là hình thang cân.
Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.
Bài 3.43: Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2 AB.
a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?
b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD.
Giải:

Ta có AP = 2AB suy ra AB = BP =
Vì ABCD là hình bình hành nên:
• AB // CD hay BP // CD
• AB = CD mà AB = BP nên BP = CD.
Tứ giác BPCD có BP // CD; BP = CD
Do đó tứ giác BPCD là hình bình hành.
b) Khi tam giác ABD vuông cân tại A thì
Ta có
Suy ra
Do đó
Vì tứ giác BPCD là hình bình hành nên BD // CP.
Suy ra
Khi đó
Do đó
Vậy khi tam giác ABD vuông cân tại A thì số đo các góc của tứ giác BPCD là:
Bài 3.44: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.59)
a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau
b) Chứng minh tứ giác APMN là một hình chữ nhật. Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC
c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh rằng tứ giác AMCQ là một hình thoi
d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?

Giải:
a) Theo đề bài, AC ⊥ MP; AC ⊥ AB.
Suy ra MP // AB nên MP // BN.
Do đó
Ta có P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB
Nên
Xét ∆CMP và ∆MBN có:
BM = CM (vì M là trung điểm của BC)
Do đó ∆CMP = ∆MBN (g.c.g).
b) Ta có
90o + 90o +
Suy ra
Tứ giác APMN có
Do đó, tứ giác APMN là một hình chữ nhật.
Suy ra MP = AN; AP = MN (các cặp cạnh tương ứng).
Mà MP = BN; CP = MN (vì ∆CMP = ∆MBN).
Do đó AP = CP; AN = BN.
Từ đó ta suy ra N là trung điểm của AB, P là trung điểm của AC.
c) Tứ giác AMCQ có:
MP = PQ (vì P là trung điểm của MQ)
AP = CP (vì P là trung điểm của AC)
Khi đó, tứ giác AMCQ có hai đường chéo AC và MQ cắt nhau tại trung điểm P của mỗi đường nên nó là hình bình hành.
Mà MQ ⊥ AC.
Do đó tứ giác AMCQ là một hình thoi.
d) Tứ giác APMN là một hình chữ nhật nên MP = AN.
Mà P là trung điểm MQ; N là trung điểm của AB.
Suy ra MQ = AB.
Lại có AB = AC (giả thiết) nên MQ = AC.
Tứ giác AMCQ có hai đường chéo AC và MQ bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm P của mỗi đường.
Do đó, tứ giác AMCQ có là hình vuông.
Bài 3.45: Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N là chân đường vuông góc hạ từ B xuống ME (H.3.60)

Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật
b) BK và NE cùng bằng hiệu khoảng cách từ M đến AC và AB (dù M thay đổi trên đường thẳng MC miễn là B nằm giữa M và C)
Giải:

Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025