Giải SGK Toán 6 chương 1, bài 5: Phép tính lũy thừa với số mũ tự nhiên - Sách Cánh diều
Giải bài tập SGK Toán 6 chương 1, bài 5: Phép tính lũy thừa với số mũ tự nhiên - Sách Cánh diều, trang 22.
Vi khuẩn E.coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần
(Nguồn: sinh học 10, NXB Giáo dục Việt Nam, 2010)
Vi khuẩn E.coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần
Giả sử lúc đầu có 1 vi khuẩn. Sau 120 phút có bao nhiêu vi khuẩn?
Giải:
- Trước khi chưa học bài Lũy thừa, em giải quyết bài toán trên như sau:
Vì cứ sau 20 phút, vi khuẩn lại phân đôi 1 lần nên sau 20 phút đầu, từ 1 vi khuẩn ta có 2 vi khuẩn.
Sau 20 phút tiếp theo (tức là sau 40 phút), từ 2 vi khuẩn phân đôi thành 2 . 2 = 4 vi khuẩn.
Sau 20 phút tiếp (tức là sau 60 phút), từ 4 vi khuẩn phân đôi thành 4 . 2 = 8 vi khuẩn.
Sau 20 phút tiếp (tức là sau 80 phút), từ 8 vi khuẩn phân đôi thành 8 . 2 = 16 vi khuẩn.
Tiếp tục sau 20 phút nữa (tức là sau 100 phút), từ 16 vi khuẩn phân đôi thành 16 . 2 = 32 vi khuẩn.
Sau 20 phút nữa (tức là sau 120 phút), từ 32 vi khuẩn phân đôi thành 32 . 2 = 64 vi khuẩn.
Vậy sau 120 phút có tất cả 64 vi khuẩn.
- Sau khi học xong bài Lũy thừa, em có thể giải quyết bài toán như sau:
120 phút hơn 20 phút số lần là: 120 : 20 = 6 (lần)
Cứ sau 20 phút, vi khuẩn lại phân đôi 1 lần, tức là gấp 2 lần số lượng ban đầu.
Vậy sau 120 phút, có tất cả: 26= 64 vi khuẩn.
Viết và tính các lũy thừa sau:
a) Năm mũ hai;
b) Hai lũy thừa bảy;
c) Lũy thừa bậc ba của sáu.
Giải:
a) 52= 5 . 5 = 25
b) 27= 2 . 2 . 2 . 2 . 2 . 2 . 2 = 128
c) 63= 6 .6 . 6 = 216
Bài tập 2:
Viết các số sau dưới dạng lũy thừa với cơ số cho trước:
a) 25, cơ số 5;
b) 64, cơ số 4.
Giải:
a) 25 = 5. 5 = 52
b) 64 = 4 . 4 . 4 = 43
Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:
a) 25 . 64
b) 20 . 5 . 103
Giải:
a) 25 . 64 = 25.26 = 25+6 = 211
b) 20 . 5 . 103 = 100 . 103 = 102 . 103 = 102+3 = 105
Bài tập 4:
Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:
a) 65 : 6
b) 128 : 23
Giải:
a) 65 : 6 = 65 : 61 = 65−1 = 64
b) 128 : 23 = 27 : 23 = 27−3 = 24
Bài 1 - Trang 24: (Toán 6 tập 1 sách Cánh Diều)
Viết các tích sau dưới dạng lũy thừa:
a) 5 . 5 . 5 . 5;
b) 9 . 9 . 9 . 9 . 9 . 9 . 9;
c) 7 . 7 . 7 . 7 . 7;
d) a . a . a . a . a . a . a . a
Giải:
a) 5 . 5. 5 . 5 = 54. (vì trong tích có 4 thừa số 5)
b) 9 . 9 . 9 . 9 . 9 . 9 . 9 = 97. (vì trong tích có 7 thừa số 9)
c) 7 . 7 . 7 . 7 . 7 = 75. (vì trong tích có 5 thừa số 7)
d) a . a . a . a . a . a . a . a = a8. (vì trong tích có 8 thừa số a)
Bài 2 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
Xác định cơ số, số mũ và tính mỗi lũy thừa sau:
25, 52,92, 110, 101
Giải:
- 25 có cơ số là 2, số mũ là 5 và
25 = 2 . 2 . 2 . 2 . 2 = 4 . 2 . 2 . 2 = 8 . 2 . 2 = 16 . 2 = 32
- 52 có cơ số là 5, số mũ là 2 và 52 = 5 . 5 = 25
- 92 có cơ số là 9, số mũ là 2 và 92 = 9 . 9 = 81
- 110 có cơ số là 1, số mũ là 10 và
110 = 1.1.1.1.1.1.1.1.1.1 = 1
- 101 có cơ số là 10, số mũ là 1 và 101 = 10. (một số bất kì lũy thừa 1 thì bằng chính nó).
Bài 3 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
Viết các số sau dưới dạng lũy thừa với cơ số cho trước:
a) 81, cơ số 3;
b) 81, cơ số 9;
c) 64, cơ số 2;
d) 100 000 000, cơ số 10.
Giải:
a) Để viết 81 dưới dạng lũy thừa với cơ số 3, ta tách 81 thành tích của các thừa số 3:
81 = 3 . 27 = 3 . 3 . 9 = 3 . 3 . 3 . 3 = 34.
Vậy 81 = 34.
b) Để viết 81 dưới dạng lũy thừa với cơ số 9, ta tách 81 thành tích của các thừa số 9:
81 = 9 . 9 = 92
Vậy 81 = 92.
c) Để viết 64 dưới dạng lũy thừa với cơ số 2, ta tách 64 thành tích của các thừa số 2:
64 = 2 . 32 = 2 . 2 . 16 = 2 . 2. 2 . 8 = 2 . 2 . 2 . 2 . 2 . 2= 26
Vậy 64 = 26.
d) Để viết 100 000 000 dưới dạng lũy thừa với cơ số 10, ta tách 100 000 000 thành tích của các thừa số 10:
100 000 000 = 10 . 10 000 000 = 10 . 10 . 1 000 000
= 10 . 10 . 10 . 100 000
= 10 . 10 . 10 . 10 . 10 000
= 10 . 10 . 10 . 10 . 10 . 1 000
= 10 . 10 . 10 . 10 . 10 . 10 . 100
= 10 . 10 . 10 . 10. 10 . 10 . 10 . 10
= 108
Vậy 100 000 000 = 108 .
Bài 4 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
a) 34.35 ; 16.29 ; 16.32 ;
b) 128 : 12 ; 243 : 34 ; 109 : 10000 ;
c) 4.86.2.83 ; 122.2.123.6 ; 63.2.64.3 .
Giải:
a) 34.35 = 34 + 5 = 39.
16.29 = (2 . 2 . 2 . 2) . 29 = 24 . 29 = 24 + 9 = 213.
16 . 32 = 24 . (2 . 2 . 2 . 2 . 2) = 24 . 25 = 24 + 5 = 29.
b) 128 : 12 = 128 : 121 = 128 - 1 = 127.
243 : 34 = (3. 81) : 34 = (3 . 3 . 27) : 34 = (3 . 3 . 3 . 3. 3) : 34 = 35 : 34 = 35 - 4 =31.
109 : 10 000 = 109 : (10 . 1 000) = 109 : (10. 10 . 100)
= 109 : (10 . 10 . 10 . 10)
= 109 : 104 = 109 - 4 = 105.
c) 4.86.2.83
= 4 . 2 . 86 . 83 (tính chất giao hoán)
= (4 . 2) . 86 . 83 (tính chất kết hợp)
= 8 . 86 . 83
= 81 . 86 . 83
= 81 + 6 . 83
= 87 . 83 = 87 + 3 = 810.
122.2.123.6
= (2. 6) . (122 . 123) (tính chất giao hoán và kết hợp)
= 12 . 122 + 3
= 121 . 125 = 121 + 5 = 126.
63.2.64.3
= (2 . 3) . (63 . 64) (tính chất giao hoán và kết hợp)
= 6 . 63 + 4
= 61 . 67 = 61 + 7 = 68.
Bài 5 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
So sánh:
a) 32 và 3.2;
b) 23 và 32;
c) 33 và 34
Giải:
a) Ta có: 32 = 3 . 3 = 9 và 3 . 2 = 6
Vì 9 > 6 nên 32 > 3 . 2
Vậy 32 > 3 . 2.
b) Ta có: 23 = 2 . 2 . 2 = 8 và 32 = 3. 3 = 9
Vì 8 < 9 nên 23 < 32
Vậy 23 < 32.
c) Ta có: 33 = 3 . 3 . 3 = 27 và 34 = 3 . 3. 3. 3 = 81
Vì 27 < 81 nên 33 < 34
Vậy 33 < 34.
Qua bài tập c) này, ta có nhận xét: Đối với lũy thừa với cơ số và số mũ là số tự nhiên thì khi so sánh hai lũy thừa cùng cơ số, lũy thừa nào có số mũ bé hơn thì bé hơn.
Bài 6 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
Khói lượng của Mặt Trời khoảng 199.1025 tấn, khối lượng của Trái Đất khoảng 6. 1021 tấn.
Nguồn: http://nssdc.gsfc.nasa.gov)
Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng của Trái Đất?
Giải:
Khối lượng Mặt Trời gấp số lần khối lượng Trái Đất là:
(199 . 1025) : (6 . 1021) = (199 : 6) . (1025 . 1021)
= 33,17 . 104 = 33,17 . 10 000 = 331 700
Vậy khối lượng Mặt Trời gấp khoảng 331 700 lần khối lượng Trái Đất.
Bài 7 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
Đố. Cho biết 112 = 121; 1112 = 12 321
Hãy dự đoán 11112 bằng bao nhiêu. Kiểm tra lại dự đoán đó
Giải:
Ta có: 112 = 121; 1112 = 12 321
Do đó ta dự đoán: 1 1112 = 1 234 321
Kiểm tra: 11112 = 1 111 . 1 111
Ta có:
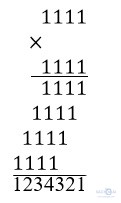
Vậy 1 1112 = 1 234 321.
(Nguồn: sinh học 10, NXB Giáo dục Việt Nam, 2010)
Vi khuẩn E.coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần
Giả sử lúc đầu có 1 vi khuẩn. Sau 120 phút có bao nhiêu vi khuẩn?
Giải:
- Trước khi chưa học bài Lũy thừa, em giải quyết bài toán trên như sau:
Vì cứ sau 20 phút, vi khuẩn lại phân đôi 1 lần nên sau 20 phút đầu, từ 1 vi khuẩn ta có 2 vi khuẩn.
Sau 20 phút tiếp theo (tức là sau 40 phút), từ 2 vi khuẩn phân đôi thành 2 . 2 = 4 vi khuẩn.
Sau 20 phút tiếp (tức là sau 60 phút), từ 4 vi khuẩn phân đôi thành 4 . 2 = 8 vi khuẩn.
Sau 20 phút tiếp (tức là sau 80 phút), từ 8 vi khuẩn phân đôi thành 8 . 2 = 16 vi khuẩn.
Tiếp tục sau 20 phút nữa (tức là sau 100 phút), từ 16 vi khuẩn phân đôi thành 16 . 2 = 32 vi khuẩn.
Sau 20 phút nữa (tức là sau 120 phút), từ 32 vi khuẩn phân đôi thành 32 . 2 = 64 vi khuẩn.
Vậy sau 120 phút có tất cả 64 vi khuẩn.
- Sau khi học xong bài Lũy thừa, em có thể giải quyết bài toán như sau:
120 phút hơn 20 phút số lần là: 120 : 20 = 6 (lần)
Cứ sau 20 phút, vi khuẩn lại phân đôi 1 lần, tức là gấp 2 lần số lượng ban đầu.
Vậy sau 120 phút, có tất cả: 26= 64 vi khuẩn.
I. Phép nâng lên lũy thừa
Bài tập 1:Viết và tính các lũy thừa sau:
a) Năm mũ hai;
b) Hai lũy thừa bảy;
c) Lũy thừa bậc ba của sáu.
Giải:
a) 52= 5 . 5 = 25
b) 27= 2 . 2 . 2 . 2 . 2 . 2 . 2 = 128
c) 63= 6 .6 . 6 = 216
Bài tập 2:
Viết các số sau dưới dạng lũy thừa với cơ số cho trước:
a) 25, cơ số 5;
b) 64, cơ số 4.
Giải:
a) 25 = 5. 5 = 52
b) 64 = 4 . 4 . 4 = 43
II. Nhân hai lũy thừa cùng cơ số
Bài tập 3:Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa:
a) 25 . 64
b) 20 . 5 . 103
Giải:
a) 25 . 64 = 25.26 = 25+6 = 211
b) 20 . 5 . 103 = 100 . 103 = 102 . 103 = 102+3 = 105
III. Chia hai lũy thừa cùng cơ số
Bài tập 4:Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:
a) 65 : 6
b) 128 : 23
Giải:
a) 65 : 6 = 65 : 61 = 65−1 = 64
b) 128 : 23 = 27 : 23 = 27−3 = 24
* Bài tập
Bài 1 - Trang 24: (Toán 6 tập 1 sách Cánh Diều)Viết các tích sau dưới dạng lũy thừa:
a) 5 . 5 . 5 . 5;
b) 9 . 9 . 9 . 9 . 9 . 9 . 9;
c) 7 . 7 . 7 . 7 . 7;
d) a . a . a . a . a . a . a . a
Giải:
a) 5 . 5. 5 . 5 = 54. (vì trong tích có 4 thừa số 5)
b) 9 . 9 . 9 . 9 . 9 . 9 . 9 = 97. (vì trong tích có 7 thừa số 9)
c) 7 . 7 . 7 . 7 . 7 = 75. (vì trong tích có 5 thừa số 7)
d) a . a . a . a . a . a . a . a = a8. (vì trong tích có 8 thừa số a)
Bài 2 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
Xác định cơ số, số mũ và tính mỗi lũy thừa sau:
25, 52,92, 110, 101
Giải:
- 25 có cơ số là 2, số mũ là 5 và
25 = 2 . 2 . 2 . 2 . 2 = 4 . 2 . 2 . 2 = 8 . 2 . 2 = 16 . 2 = 32
- 52 có cơ số là 5, số mũ là 2 và 52 = 5 . 5 = 25
- 92 có cơ số là 9, số mũ là 2 và 92 = 9 . 9 = 81
- 110 có cơ số là 1, số mũ là 10 và
110 = 1.1.1.1.1.1.1.1.1.1 = 1
- 101 có cơ số là 10, số mũ là 1 và 101 = 10. (một số bất kì lũy thừa 1 thì bằng chính nó).
Bài 3 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
Viết các số sau dưới dạng lũy thừa với cơ số cho trước:
a) 81, cơ số 3;
b) 81, cơ số 9;
c) 64, cơ số 2;
d) 100 000 000, cơ số 10.
Giải:
a) Để viết 81 dưới dạng lũy thừa với cơ số 3, ta tách 81 thành tích của các thừa số 3:
81 = 3 . 27 = 3 . 3 . 9 = 3 . 3 . 3 . 3 = 34.
Vậy 81 = 34.
b) Để viết 81 dưới dạng lũy thừa với cơ số 9, ta tách 81 thành tích của các thừa số 9:
81 = 9 . 9 = 92
Vậy 81 = 92.
c) Để viết 64 dưới dạng lũy thừa với cơ số 2, ta tách 64 thành tích của các thừa số 2:
64 = 2 . 32 = 2 . 2 . 16 = 2 . 2. 2 . 8 = 2 . 2 . 2 . 2 . 2 . 2= 26
Vậy 64 = 26.
d) Để viết 100 000 000 dưới dạng lũy thừa với cơ số 10, ta tách 100 000 000 thành tích của các thừa số 10:
100 000 000 = 10 . 10 000 000 = 10 . 10 . 1 000 000
= 10 . 10 . 10 . 100 000
= 10 . 10 . 10 . 10 . 10 000
= 10 . 10 . 10 . 10 . 10 . 1 000
= 10 . 10 . 10 . 10 . 10 . 10 . 100
= 10 . 10 . 10 . 10. 10 . 10 . 10 . 10
= 108
Vậy 100 000 000 = 108 .
Bài 4 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
a) 34.35 ; 16.29 ; 16.32 ;
b) 128 : 12 ; 243 : 34 ; 109 : 10000 ;
c) 4.86.2.83 ; 122.2.123.6 ; 63.2.64.3 .
Giải:
a) 34.35 = 34 + 5 = 39.
16.29 = (2 . 2 . 2 . 2) . 29 = 24 . 29 = 24 + 9 = 213.
16 . 32 = 24 . (2 . 2 . 2 . 2 . 2) = 24 . 25 = 24 + 5 = 29.
b) 128 : 12 = 128 : 121 = 128 - 1 = 127.
243 : 34 = (3. 81) : 34 = (3 . 3 . 27) : 34 = (3 . 3 . 3 . 3. 3) : 34 = 35 : 34 = 35 - 4 =31.
109 : 10 000 = 109 : (10 . 1 000) = 109 : (10. 10 . 100)
= 109 : (10 . 10 . 10 . 10)
= 109 : 104 = 109 - 4 = 105.
c) 4.86.2.83
= 4 . 2 . 86 . 83 (tính chất giao hoán)
= (4 . 2) . 86 . 83 (tính chất kết hợp)
= 8 . 86 . 83
= 81 . 86 . 83
= 81 + 6 . 83
= 87 . 83 = 87 + 3 = 810.
122.2.123.6
= (2. 6) . (122 . 123) (tính chất giao hoán và kết hợp)
= 12 . 122 + 3
= 121 . 125 = 121 + 5 = 126.
63.2.64.3
= (2 . 3) . (63 . 64) (tính chất giao hoán và kết hợp)
= 6 . 63 + 4
= 61 . 67 = 61 + 7 = 68.
Bài 5 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
So sánh:
a) 32 và 3.2;
b) 23 và 32;
c) 33 và 34
Giải:
a) Ta có: 32 = 3 . 3 = 9 và 3 . 2 = 6
Vì 9 > 6 nên 32 > 3 . 2
Vậy 32 > 3 . 2.
b) Ta có: 23 = 2 . 2 . 2 = 8 và 32 = 3. 3 = 9
Vì 8 < 9 nên 23 < 32
Vậy 23 < 32.
c) Ta có: 33 = 3 . 3 . 3 = 27 và 34 = 3 . 3. 3. 3 = 81
Vì 27 < 81 nên 33 < 34
Vậy 33 < 34.
Qua bài tập c) này, ta có nhận xét: Đối với lũy thừa với cơ số và số mũ là số tự nhiên thì khi so sánh hai lũy thừa cùng cơ số, lũy thừa nào có số mũ bé hơn thì bé hơn.
Bài 6 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
Khói lượng của Mặt Trời khoảng 199.1025 tấn, khối lượng của Trái Đất khoảng 6. 1021 tấn.
Nguồn: http://nssdc.gsfc.nasa.gov)
Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng của Trái Đất?
Giải:
Khối lượng Mặt Trời gấp số lần khối lượng Trái Đất là:
(199 . 1025) : (6 . 1021) = (199 : 6) . (1025 . 1021)
= 33,17 . 104 = 33,17 . 10 000 = 331 700
Vậy khối lượng Mặt Trời gấp khoảng 331 700 lần khối lượng Trái Đất.
Bài 7 - Trang 25: (Toán 6 tập 1 sách Cánh Diều)
Đố. Cho biết 112 = 121; 1112 = 12 321
Hãy dự đoán 11112 bằng bao nhiêu. Kiểm tra lại dự đoán đó
Giải:
Ta có: 112 = 121; 1112 = 12 321
Do đó ta dự đoán: 1 1112 = 1 234 321
Kiểm tra: 11112 = 1 111 . 1 111
Ta có:
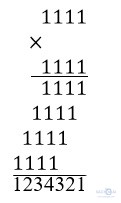
Vậy 1 1112 = 1 234 321.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
 Giải SGK Toán 6 chương 1, bài 6: Thứ tự thực hiện các phép tính - Sách Cánh diều
Giải SGK Toán 6 chương 1, bài 6: Thứ tự thực hiện các phép tính - Sách Cánh diều