Các kiểu dữ liệu đơn giản trong Pascal
1. KHÁI NIỆM CHUNG
Dữ liệu (DATA) là tất cả những gì mà máy tính xử lí.
Theo Niklaus Wirth: CHƯƠNG TRÌNH = THUẬT TOÁN + CẤU TRÚC DỮ LIỆU
Một kiểu dữ liệu (Data type) là một sự qui định về hình dạng, cấu trúc và giá trị của dữ liệu cũng như cách biểu diễn và cách xử lí dữ liệu.
Dữ liệu (DATA) là tất cả những gì mà máy tính xử lí.
Theo Niklaus Wirth: CHƯƠNG TRÌNH = THUẬT TOÁN + CẤU TRÚC DỮ LIỆU
Một kiểu dữ liệu (Data type) là một sự qui định về hình dạng, cấu trúc và giá trị của dữ liệu cũng như cách biểu diễn và cách xử lí dữ liệu.
Trong Pascal các kiểu dữ liệu nhìn chung được chia thành hai loại chính :
- Kiểu đơn giản (Simple type)
- Kiểu có cấu trúc (Structure type)
Trong phần này chúng ta chỉ xét các kiểu dữ liệu đơn giản.
Kiểu dữ liệu đơn giản của Pascal bao gồm :
- Kiểu số nguyên (Integer)
- Kiểu số thực (Real)
-. Kiểu logic (Boolean)
- Kiểu kí tự (Char).
2. KIỂU SỐ NGUYÊN (INTEGER)
a) Kiểu số nguyên thuộc Z được định nghĩa vôi các từ khóa sau :
b) Các phép toán số học đối với số nguyên :
3. KIỂU SỐ THỰC (REAL)
a) Kiểu số thực thuộc tập R được định nghĩa với từ khóa REAL :
• CÁCH 1 : Viết theo kiểu thập phân bình thường.
- Ví dụ : 3.14
-0.004
Lưu ý: Dùng dấu chấm thay cho dấu phẩy trong cách viết của Việt Nam.
• CÁCH 2: Viết theo kiểu thập phân có phần mũ và phần định trị.
» Ví dụ : 3.93 E+2 (= 393)
3 93 E -3 (=0,00393)
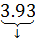
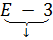 (=0,00393)
(=0,00393)
Phần định trị Phần mũ
b) Các hàm số học dùng cho số nguyên và số thực :
- Chú thích :
- TRUNC(x) : Số nguyên lớn nhất không vượt quá x
- ROUND(x) : Số nguyên gần x nhất.
4. Kiểu LOGIC (BOOLEAN)
a) Định nghĩa :
Một dữ liệu thuộc kiểu BOOLEAN là một đại lượng chỉ có thể nhận một trong hai giá trị logic TRUE hoặc FALSE.
• Ví dụ : Giả sử có khai báo.
Var
Làm được_được : Boolean.
Thì ta có thể làm các phép gán
Làm được := False ; {Sai}
Hoặc
Làm_được := True ; {Đúng}
b) Các phép toán trên kiểu Boolean :
c) Các phép toán quan hệ cho kết quả kiểu Boolean :
5. KIỂU KÍ TỰ (CHAR)
a) Định nghĩa :
Các dữ liệu có dạng chữ viết (kí tự) được khai báo bởi từ khóa CHAR.
- Ví dụ : Giả sử có khai báo
Var
X : Char ;
Thì ta có thể làm các phép gán sau :
X := 'A' ;
hoặc :
X := '?’ ;
b) Để tiện trao đổi thông tin cần phải sắp xếp, đánh số thứ tự các kí tự. Mỗi cách sắp xếp như vậy gọi là một bảng mã. Thông dụng nhất là bảng mã ASCII (American Standar Code For Information Interchange).
- Ví dụ :
c) Các hàm chuẩn liên quan đến kiểu kí tự:
- Kiểu đơn giản (Simple type)
- Kiểu có cấu trúc (Structure type)
Trong phần này chúng ta chỉ xét các kiểu dữ liệu đơn giản.
Kiểu dữ liệu đơn giản của Pascal bao gồm :
- Kiểu số nguyên (Integer)
- Kiểu số thực (Real)
-. Kiểu logic (Boolean)
- Kiểu kí tự (Char).
2. KIỂU SỐ NGUYÊN (INTEGER)
a) Kiểu số nguyên thuộc Z được định nghĩa vôi các từ khóa sau :
| TỪ KHÓA | PHẠM VI |
| INTEGER | -32768 đến 32767 |
| BYTE | 0 đến 25 |
| WORD | 0 đến 65535 |
| SHORTINT | -128 đến 127 |
| LONGINT | -2147483648 đến 2147483647 |
b) Các phép toán số học đối với số nguyên :
| KÍ HIỆU | Ý NGHĨA |
| DIV | Chia lấy phần nguyên |
| MOD | Chia lấy phần dư |
| + | Cộng |
| - | Trừ |
| * | Nhân |
| / | Chia cho kết quả là số thực |
3. KIỂU SỐ THỰC (REAL)
a) Kiểu số thực thuộc tập R được định nghĩa với từ khóa REAL :
| Từ khóa | Phạm vi |
| REAL | 2.9xl0’39 đến 1.7x1038 |
- Ví dụ : 3.14
-0.004
Lưu ý: Dùng dấu chấm thay cho dấu phẩy trong cách viết của Việt Nam.
• CÁCH 2: Viết theo kiểu thập phân có phần mũ và phần định trị.
» Ví dụ : 3.93 E+2 (= 393)
3 93 E -3 (=0,00393)
Phần định trị Phần mũ
b) Các hàm số học dùng cho số nguyên và số thực :
| Kí hiệu | Ý nghĩa |
| ABS(x) | |x|: lấy giá trị tuyệt đối của x |
| SQR(x) | x2 : lấy bình phương của x |
| SQRT(x) | |
| SIN(x), COS(x) | sin(x), cos(x) |
| ARCTAN(x) | arctang(x) |
| LN(x) | logex (e ≈ 2,71828) |
| EXP(x) | ex |
| SUCC(n) | n + 1 |
| PRED(n) | n - 1 |
| ODD(n) | TRUE nếu n lẻ, FALSE nếu n chẵn |
| TRUNC(x) | Lấy phần nguyên của x |
| ROUND(x) | Làm tròn x |
- TRUNC(x) : Số nguyên lớn nhất không vượt quá x
- ROUND(x) : Số nguyên gần x nhất.
4. Kiểu LOGIC (BOOLEAN)
a) Định nghĩa :
Một dữ liệu thuộc kiểu BOOLEAN là một đại lượng chỉ có thể nhận một trong hai giá trị logic TRUE hoặc FALSE.
• Ví dụ : Giả sử có khai báo.
Var
Làm được_được : Boolean.
Thì ta có thể làm các phép gán
Làm được := False ; {Sai}
Hoặc
Làm_được := True ; {Đúng}
b) Các phép toán trên kiểu Boolean :
| A | B | A AND B | A | B | A OR B | |
| TRUE TRUE FALSE FALSE |
TRUE FALSE TRUE FALSE |
TRUE FALSE FALSE FALSE |
TRUE TRUE FALSE FALSE |
TRUE FALSE TRUE FALSE |
TRUE TRUE TRUE FALSE |
| A | NOT A |
| TRUE FALSE |
FALSE TRUE |
c) Các phép toán quan hệ cho kết quả kiểu Boolean :
| Kí hiệu | Ý nghĩa |
| < > | Khác nhau |
| = | Bằng nhau |
| >= | Lớn hơn hoặc bằng |
| <= | Nhỏ hơn hoặc bằng |
| > | Lớn hơn |
| < | Nhỏ hơn |
5. KIỂU KÍ TỰ (CHAR)
a) Định nghĩa :
Các dữ liệu có dạng chữ viết (kí tự) được khai báo bởi từ khóa CHAR.
- Ví dụ : Giả sử có khai báo
Var
X : Char ;
Thì ta có thể làm các phép gán sau :
X := 'A' ;
hoặc :
X := '?’ ;
b) Để tiện trao đổi thông tin cần phải sắp xếp, đánh số thứ tự các kí tự. Mỗi cách sắp xếp như vậy gọi là một bảng mã. Thông dụng nhất là bảng mã ASCII (American Standar Code For Information Interchange).
- Ví dụ :
| Số thứ tự | Kí tự | Số thứ tự | Kí tự |
| 7 | BEL | 65 | A |
| 32 | SPACE | 66 | B |
| 43 | + | 90 | z |
| 48 | 0 | 97 | a |
| 49 | 1 | 98 | b |
| 61 | = | 122 | z |
c) Các hàm chuẩn liên quan đến kiểu kí tự:
| Kí hiệu | Ý nghĩa |
| ORD(x) | Cho số thứ tự của kí tự x trong bảng mã |
| CHR(n) hay #n | Cho kí tự có số thứ tự là n |
| PRED(x) | Cho kí tự đứng trước x |
| SUCC(x) | Cho kí tự đứng sau x |
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
 Lập trình trò chơi đổi màu bi trong Pascal
Lập trình trò chơi đổi màu bi trong Pascal