Giải SGK Toán 7 sách Kết nối tri thức: Luyện tập chung trang 58
Giải SGK Toán 7 sách Kết nối tri thức: Luyện tập chung trang 58
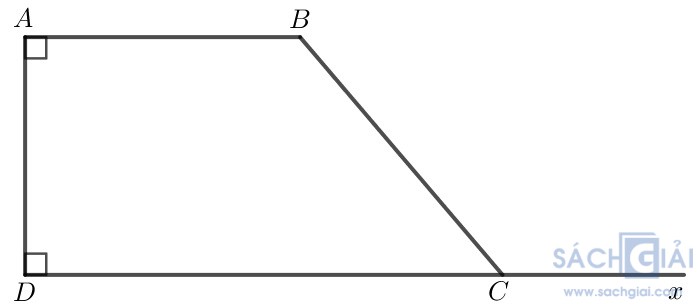
Bài 3.27 - Trang 58: Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó.
Giải:

Bài 3.28 - Trang 58: Vẽ hình minh họa và viết giả thiết, kết luận của định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.
Giải:

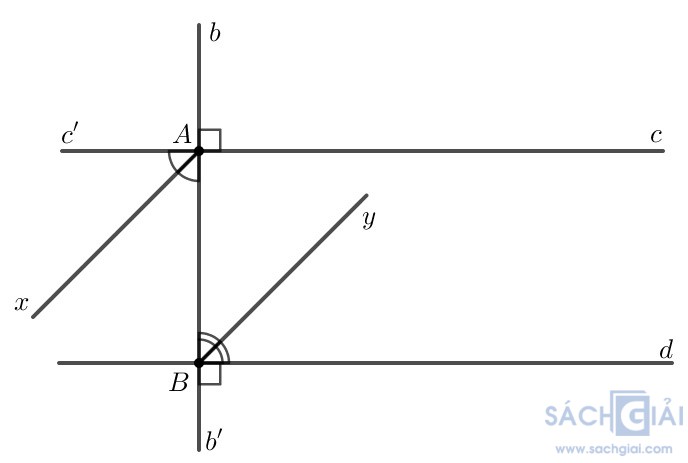
Bài 3.29 - Trang 58 : Kẻ các tia phân giác Ax, By của một cặp góc so le trong tạo bởi đường thẳng b vuông góc với hai đường thẳng song song c, d (H 3.48). Chứng minh rằng hai tia phân giác đó nằm cùng trên hai đường thẳng song song.
Giải:

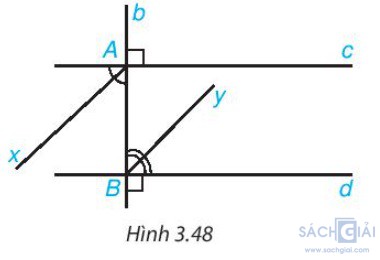
Bài 3.30 - Trang 58: Cho hai đường thẳng phân biệt a, b cùng vuông góc với đường thẳng c; d là một đường thẳng khác khác c và d vuông góc với a. Chứng minh rằng:
a) a // b
b) c // d
c) b ⊥ d
Giải:
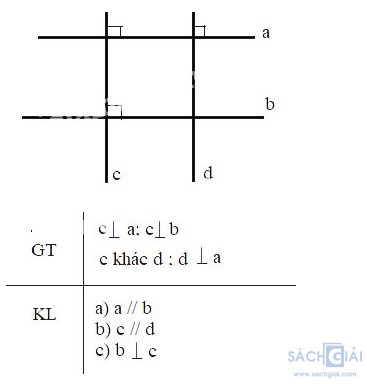
a) Vì c ⊥ a;c ⊥ b => a//b (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
b) Vì a⊥ c;a ⊥ d => c//d (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
c) Vì b ⊥ c;c//d => b ⊥ c (đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia)
Bài 3.31 - Trang 58: Cho hình 3.49. Chứng minh rằng:
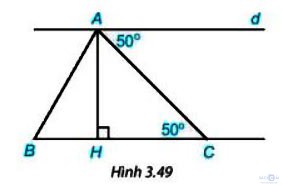
a) d // BC
b) d ⊥ AH
c) Trong các kết luận trên, kết luận nào được suy ra từ tính chất của hai đường thẳng song song, kết luận nào được suy ra từ dấu hiệu nhận biết hai đường thẳng song song?
Giải:
a) Ta có
Mà hai góc này ở vị trí so le trong nên d // BC.
Vậy d // BC.
b) Áp dụng định lí: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại” ta có:
Do BC ⊥ AH, BC // d nên d ⊥ AH
c) Trong hai kết luận trên, kết luận d // BC được suy ra từ dấu hiệu nhận biết hai đường thẳng song song.
Kết luận d ⊥ AH được suy ra từ tính chất hai đường thẳng song song.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025