Giải SGK Toán 7 sách Kết nối tri thức, bài 11: Định lí và chứng minh định lí
Giải SGK Toán 7 sách Kết nối tri thức, bài 11: Định lí và chứng minh định lí - Trang 55, ...
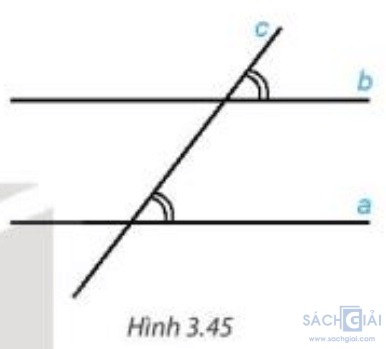
Mở đầu trang 55: Trong Bài 10, ta đã dùng cách đo đạc để kiểm nghiệm tính chất sau là đúng:
“Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau” (H.3.45).
Tuy nhiên, đo đạc chỉ cho ta kết quả gần đúng và chỉ trong một trường hợp cụ thể.
Vậy có cách nào để chắc chắn rằng tính chất đó đúng cho mọi trường hợp không?
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Giải:
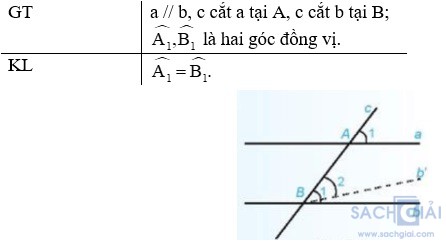
Chứng minh:
Qua điểm B kẻ đường thẳng b' sao cho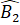 =
= 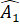
Khi đó đường thẳng c tạo với hai đường thẳng a và b' hai góc đồng vị bằng nhau
Theo dấu hiệu nhận biết hai đường thẳng song song ta có a và b' song song với nhau. Suy ra qua B có hai đường thẳng b, b' cùng song song với a. Theo tiên đề Euclid, b' trùng b. Từ đó suy ra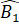 =
= 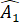 (vì cùng bằng
(vì cùng bằng 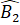 )
)
Luyện tập 1 - Trang 56: Vẽ hình và viết giả thiết, kết luận của định lí: “Hai góc đối đỉnh thì bằng nhau”.
Giải:
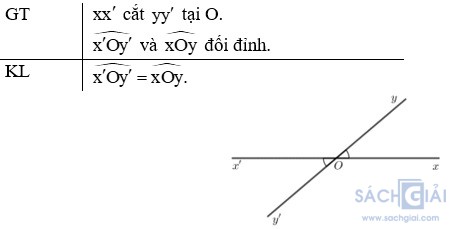
Luyện tập 2 - Trang 57: Em hãy chứng minh định lí: “Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”.
Giải:
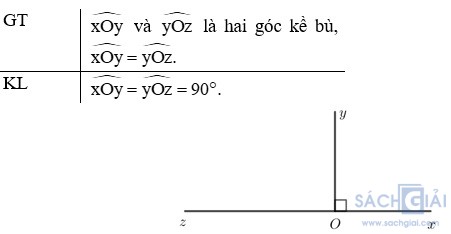
Chứng minh:
Do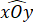 và
và 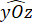 là hai góc kề bù nên
là hai góc kề bù nên 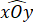 +
+ 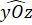 = 180o
= 180o
Mà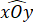 =
= 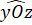 nên
nên 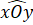 +
+ 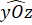 =
= 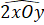 = 180o
= 180o
Do đó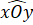 =
= 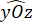 = 90o
= 90o
Tranh luận trang 57: Hình tròn: Hai góc đối đỉnh thì chắc chắn bằng nhau rồi. Liệu hai góc bằng nhau thì có đối đỉnh không nhỉ?
Hình vuông: Tớ nghĩ đó là điều không đúng! Nhưng làm thế nào để khẳng định điều đó không đúng nhỉ?
Em có ý kiến gì về hai ý kiến trên?
Giải:
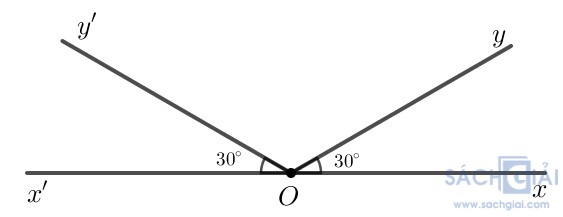
Hai góc bằng nhau thì chưa chắc đối đỉnh.
Hình vẽ bên dưới ta có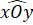 ='
='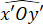 = 30o nhưng hai góc này không đối đỉnh.
= 30o nhưng hai góc này không đối đỉnh.
“Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau” (H.3.45).
Tuy nhiên, đo đạc chỉ cho ta kết quả gần đúng và chỉ trong một trường hợp cụ thể.
Vậy có cách nào để chắc chắn rằng tính chất đó đúng cho mọi trường hợp không?

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Giải:

Chứng minh:
Qua điểm B kẻ đường thẳng b' sao cho
Khi đó đường thẳng c tạo với hai đường thẳng a và b' hai góc đồng vị bằng nhau
Theo dấu hiệu nhận biết hai đường thẳng song song ta có a và b' song song với nhau. Suy ra qua B có hai đường thẳng b, b' cùng song song với a. Theo tiên đề Euclid, b' trùng b. Từ đó suy ra
Luyện tập 1 - Trang 56: Vẽ hình và viết giả thiết, kết luận của định lí: “Hai góc đối đỉnh thì bằng nhau”.
Giải:
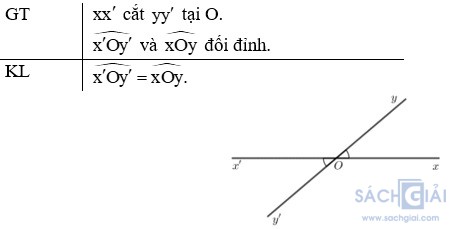
Luyện tập 2 - Trang 57: Em hãy chứng minh định lí: “Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”.
Giải:
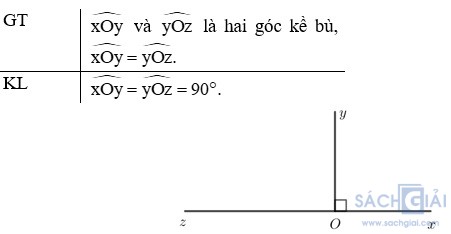
Chứng minh:
Do
Mà
Do đó
Tranh luận trang 57: Hình tròn: Hai góc đối đỉnh thì chắc chắn bằng nhau rồi. Liệu hai góc bằng nhau thì có đối đỉnh không nhỉ?
Hình vuông: Tớ nghĩ đó là điều không đúng! Nhưng làm thế nào để khẳng định điều đó không đúng nhỉ?
Em có ý kiến gì về hai ý kiến trên?
Giải:
Hai góc bằng nhau thì chưa chắc đối đỉnh.
Hình vẽ bên dưới ta có

Giải bài tập trang 57.
Bài 3.24 - Trang 57: Có thể coi định lí “Hai đường thẳng phân biệt cùng vuông góc với một đương thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?
Giải:
Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.
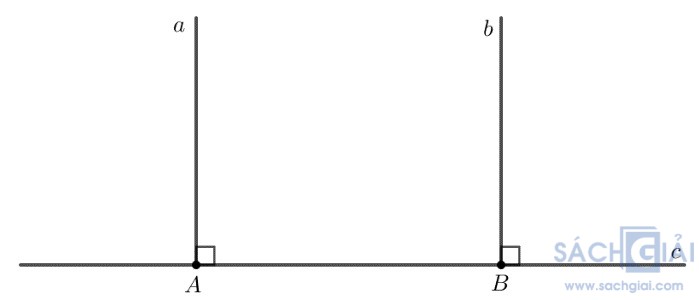
Trong hình vẽ trên, ta có hai đường thẳng a và b cùng vuông góc với đường thẳng c.
Giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.
Do đường thẳng a và đường thẳng b vuông góc với đường thẳng c nên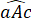 =
= 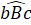 = 90o
= 90o
Mà hai góc này ở vị trí đồng vị nên a song song với b.
Vậy ta có điều phải chứng minh.
Bài 3.25 - Trang 5: Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?
Giải:
Trong hình vẽ trên, ta có hai đường thẳng a và b song song với nhau.
Đường thẳng c vuông góc với đường thẳng a.
Giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.
Do đường thẳng a vuông góc với đường thẳng c nên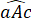 = 90o
= 90o
Do đường thẳng a song song với đường thẳng b nên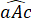 =
= 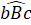 (hai góc đồng vị)
(hai góc đồng vị)
Do đó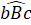 = 90o
= 90o
Vậy đường thẳng b vuông góc với đường thẳng c.
Bài 3.26 - Trang 57: Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây đúng?
(1) Nếu Ot là tia phân giác của góc xOy thì \widehat {xOt} = \widehat {tOy}
(2) Nếu tia Ot thỏa mãn \widehat {xOt} = \widehat {tOy} thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng. Gợi ý: Xét tia đối của một tia phân giác.
Giải:
(1) đúng vì Ot là tia phân giác của góc xOy thì \widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy}
(2) sai vì:
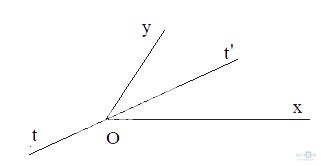
Ta có: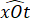 =
= 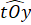 nhưng Ot không là tia phân giác của góc xOy
nhưng Ot không là tia phân giác của góc xOy
Xét tia Ot’ là tia đối của tia Ot thì Ot’ là tia phân giác của góc xOy.
Giải:
Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.

Trong hình vẽ trên, ta có hai đường thẳng a và b cùng vuông góc với đường thẳng c.
Giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.
Do đường thẳng a và đường thẳng b vuông góc với đường thẳng c nên
Mà hai góc này ở vị trí đồng vị nên a song song với b.
Vậy ta có điều phải chứng minh.
Bài 3.25 - Trang 5: Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?
Giải:
Trong hình vẽ trên, ta có hai đường thẳng a và b song song với nhau.
Đường thẳng c vuông góc với đường thẳng a.
Giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.
Do đường thẳng a vuông góc với đường thẳng c nên
Do đường thẳng a song song với đường thẳng b nên
Do đó
Vậy đường thẳng b vuông góc với đường thẳng c.
Bài 3.26 - Trang 57: Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây đúng?
(1) Nếu Ot là tia phân giác của góc xOy thì \widehat {xOt} = \widehat {tOy}
(2) Nếu tia Ot thỏa mãn \widehat {xOt} = \widehat {tOy} thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng. Gợi ý: Xét tia đối của một tia phân giác.
Giải:
(1) đúng vì Ot là tia phân giác của góc xOy thì \widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy}
(2) sai vì:

Ta có:
Xét tia Ot’ là tia đối của tia Ot thì Ot’ là tia phân giác của góc xOy.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025