Giải SGK Toán 7 sách Kết nối tri thức, bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Giải SGK Toán 7 sách Kết nối tri thức, bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác - Trang 70, ...
Mở đầu trang 70: Trong thực tế, nhiều khi ta không thể đo được hết các cạnh của hai tam giác để khẳng định được chúng có bằng nhau hay không. Khi đó, có cách nào khác giúp ta biết được điều đó?
Giải:
Chúng ta có thêm 2 cách khác để chứng minh hai tam giác bằng nhau như sau:
- Cách 1: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Cách 2: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Giải:
Chúng ta có thêm 2 cách khác để chứng minh hai tam giác bằng nhau như sau:
- Cách 1: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Cách 2: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
1. Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (C-G-C)
Hoạt động 1 - Trang 70: Vẽ 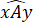 = 60o . Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm.
= 60o . Lấy điểm B trên tia Ax và điểm C trên tia Ay sao cho: AB = 4 cm, AC = 3 cm.
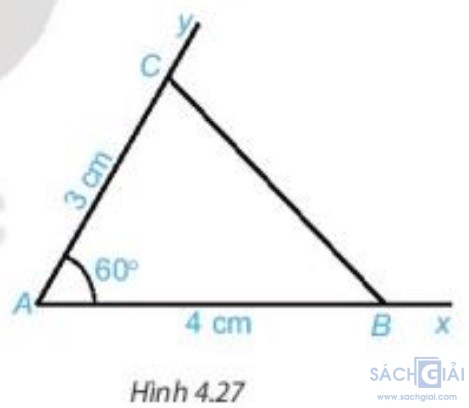
Nối điểm B với điểm C ta được tam giác ABC (H.4.27). Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.
Giải:
Dùng thước thẳng có vạch chia ta đo được độ dài cạnh BC của tam giác ABC xấp xỉ 3,6 cm.
HĐ2 trang 70:Vẽ thêm tam giác A′B′C′ với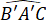 = 60o, A′B′=4 cm và A′C′ = 3cm (H.4.28).
= 60o, A′B′=4 cm và A′C′ = 3cm (H.4.28).
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và A′B′C′
- Hai tam giác ABC và A′B′C′ có bằng nhau không?
- Độ dài các cạnh BC và B'C' của hai tam giác em vừa vẽ có bằng các cạnh BC và B'C' của hai tam giác các bạn khác vẽ không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
Giải:
Thực hiện tương tự trong Hoạt động 1, ta vẽ hình như sau:
Bước 1. Vẽ '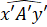 = 60o
= 60o
Bước 2. Lấy điểm B′ trên A′y′ sao cho A′B′ = 4cm và lấy điểm C′ trên A′x′ sao cho
A′C′ = 3cm.
Bước 3. Nối điểm B′ và C′ ta được tam giác A′B′C′
Vẽ thêm tam giác A'B'C' với góc B'A'C'=60 độ, A'B'=4cm và A'C'=3cm (H.4.28)
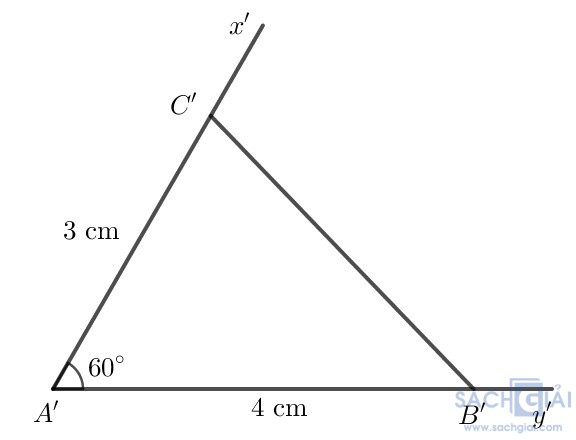
Dùng thước thẳng có vạch chia ta đo được:
AB = A'B' = 4cm, AC = A'C' = 3cm, BC = B'C' ≈ 3,6 cm
- Xét hai tam giác ABC và A′B′C′ có:
AB = A′B′ (chứng minh trên).
BC = B′C′ (chứng minh trên).
Do đó ΔABC = ΔA′B′C′ (c – c – c).
- Độ dài các cạnh BC và B'C' của hai tam giác em vừa vẽ bằng các cạnh BC và B'C' của hai tam giác các bạn khác vẽ.
- Hai tam giác em vừa vẽ bằng hai tam giác mà các bạn khác vẽ.
Câu hỏi - Trang 71: Trong Hình 4.29, hai tam giác nào bằng nhau?
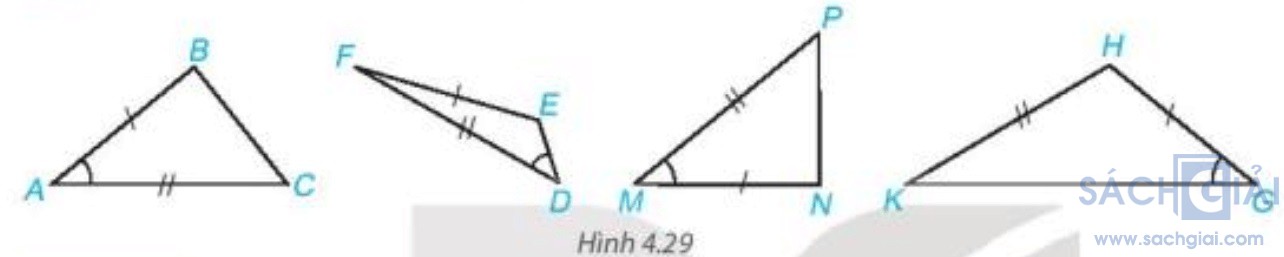
Giải:
Xét hai tam giác ABC và MNP có:
AB = MN (theo giả thiết).
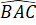 =
= 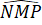 (theo giả thiết).
(theo giả thiết).
AC = MP (theo giả thiết).
Do đó ΔABC = ΔMNP (c – g – c).
Luyện tập 1 - Trang 71: Hai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao?
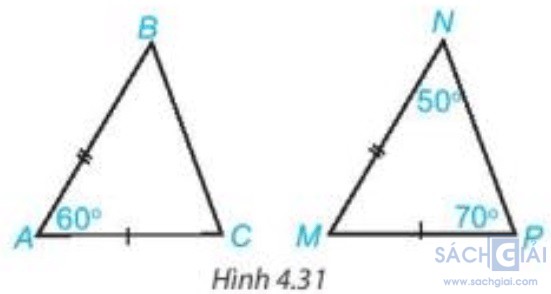
Giải:
Xét tam giác MNP có M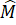 + N
+ N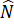 + P
+ P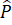 = 180o
= 180o
Do đó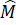 = 180o -
= 180o - 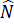 -
- 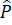 = 180o – 50o – 70o = 60o
= 180o – 50o – 70o = 60o
Xét hai tam giác ABC và MNP có:
AB = MN (theo giả thiết).
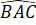 =
= 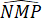 (cùng bằng 60o).
(cùng bằng 60o).
AC = MP (theo giả thiết).
Vậy ΔABC = ΔMNP (c – g – c).
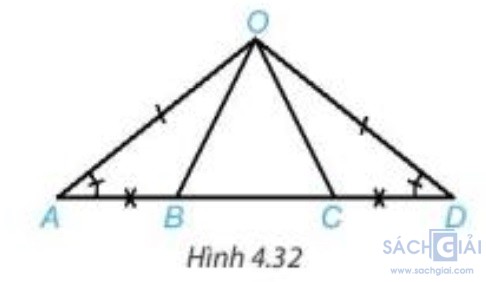
Vận dụng trang 71: Cho Hình 4.32, biết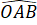 =
= 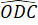 OA = OD và AB = CD. Chứng minh rằng:
OA = OD và AB = CD. Chứng minh rằng:
a) AC = DB;
b) ΔOAC = ΔODB.
Giải:
a) Do AB = CD nên AB + BC = CD + BC.
hay AC = DB.
Vậy AC = DB.
b) Xét hai tam giác OAC và ODB có:
OA = OD (theo giả thiết).
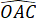 =
= 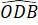 (theo giả thiết).
(theo giả thiết).
AC = BD (chứng minh trên).
Vậy ΔOAC = ΔODB (c – g – c).
Nối điểm B với điểm C ta được tam giác ABC (H.4.27). Dùng thước thẳng có vạch chia đo độ dài cạnh BC của tam giác ABC.

Giải:
Dùng thước thẳng có vạch chia ta đo được độ dài cạnh BC của tam giác ABC xấp xỉ 3,6 cm.
HĐ2 trang 70:Vẽ thêm tam giác A′B′C′ với
Dùng thước thẳng có vạch chia hoặc compa để so sánh độ dài các cạnh tương ứng của hai tam giác ABC và A′B′C′
- Hai tam giác ABC và A′B′C′ có bằng nhau không?
- Độ dài các cạnh BC và B'C' của hai tam giác em vừa vẽ có bằng các cạnh BC và B'C' của hai tam giác các bạn khác vẽ không?
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ không?
Giải:
Thực hiện tương tự trong Hoạt động 1, ta vẽ hình như sau:
Bước 1. Vẽ '
Bước 2. Lấy điểm B′ trên A′y′ sao cho A′B′ = 4cm và lấy điểm C′ trên A′x′ sao cho
A′C′ = 3cm.
Bước 3. Nối điểm B′ và C′ ta được tam giác A′B′C′
Vẽ thêm tam giác A'B'C' với góc B'A'C'=60 độ, A'B'=4cm và A'C'=3cm (H.4.28)

Dùng thước thẳng có vạch chia ta đo được:
AB = A'B' = 4cm, AC = A'C' = 3cm, BC = B'C' ≈ 3,6 cm
- Xét hai tam giác ABC và A′B′C′ có:
AB = A′B′ (chứng minh trên).
BC = B′C′ (chứng minh trên).
Do đó ΔABC = ΔA′B′C′ (c – c – c).
- Độ dài các cạnh BC và B'C' của hai tam giác em vừa vẽ bằng các cạnh BC và B'C' của hai tam giác các bạn khác vẽ.
- Hai tam giác em vừa vẽ bằng hai tam giác mà các bạn khác vẽ.
Câu hỏi - Trang 71: Trong Hình 4.29, hai tam giác nào bằng nhau?

Giải:
Xét hai tam giác ABC và MNP có:
AB = MN (theo giả thiết).
AC = MP (theo giả thiết).
Do đó ΔABC = ΔMNP (c – g – c).
Luyện tập 1 - Trang 71: Hai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao?

Giải:
Xét tam giác MNP có M
Do đó
Xét hai tam giác ABC và MNP có:
AB = MN (theo giả thiết).
AC = MP (theo giả thiết).
Vậy ΔABC = ΔMNP (c – g – c).
Vận dụng trang 71: Cho Hình 4.32, biết
a) AC = DB;
b) ΔOAC = ΔODB.

Giải:
a) Do AB = CD nên AB + BC = CD + BC.
hay AC = DB.
Vậy AC = DB.
b) Xét hai tam giác OAC và ODB có:
OA = OD (theo giả thiết).
AC = BD (chứng minh trên).
Vậy ΔOAC = ΔODB (c – g – c).
2. Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (G-C-G)
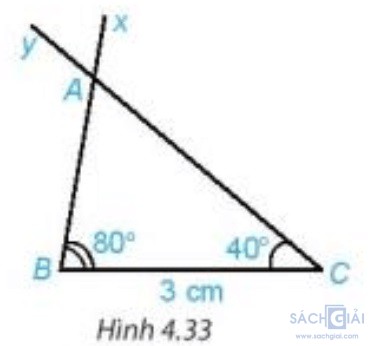
Hoạt động 3 - Trang 72: Vẽ đoạn thẳng BC = 3 cm. Vẽ hai tia Bx và Cy sao cho 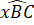 = 80o,
= 80o, 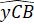 = 40o như Hình 4.33.
= 40o như Hình 4.33.
Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33). Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC.
Giải:
Dùng thước thẳng có vạch chia, ta đo được độ dài cạnh AB xấp xỉ 2,2 cm và độ dài cạnh AC xấp xỉ 3,4 cm.
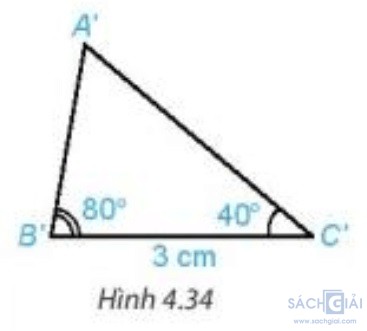
Hoạt động 4 - Trang 72: Vẽ thêm tam giác A′B′C′ sao cho B′C′= 3cm,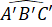 = 80o ,
= 80o , 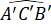 = 40o (H.4.34).
= 40o (H.4.34).
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác ABC và A′B′C′.
Hai tam giác ABC và A′B′C′ có bằng nhau không?
Giải:
Tương tự Hoạt động 3, ta vẽ hình như sau:
Bước 1. Vẽ đoạn thẳng B′C′ = 3cm
Bước 2. Dùng thước đo độ, vẽ hai tia
B′x′ và C′y′ sao cho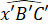 = 80o,
= 80o, 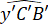 = 40o
= 40o
Bước 3. Lấy giao điểm A′ của hai tia B′x′ và C′y′ ta được tam giác A′B′C′
Vẽ thêm tam giác A'B'C' sao cho B'C'=3cm, góc A'B'C'=80 độ, góc A'C'B'=40 độ
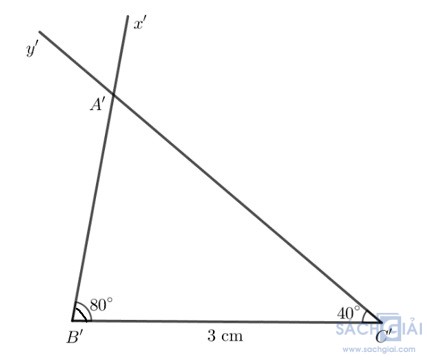
- Dùng thước thẳng có vạch chia, ta đo được AB = A'B' ≈ 2,2 cm; AC = A'C' ≈ 3,4cm và BC = B'C' = 3cm.
- Xét hai tam giác ABC và A′B′C′ có:
AB = A′B′ (chứng minh trên).
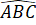 =
= 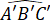 (cùng bằng 80o).
(cùng bằng 80o).
BC = B'C' (chứng minh trên).
Vậy ΔABC = ΔA'B'C' (c – g – c).
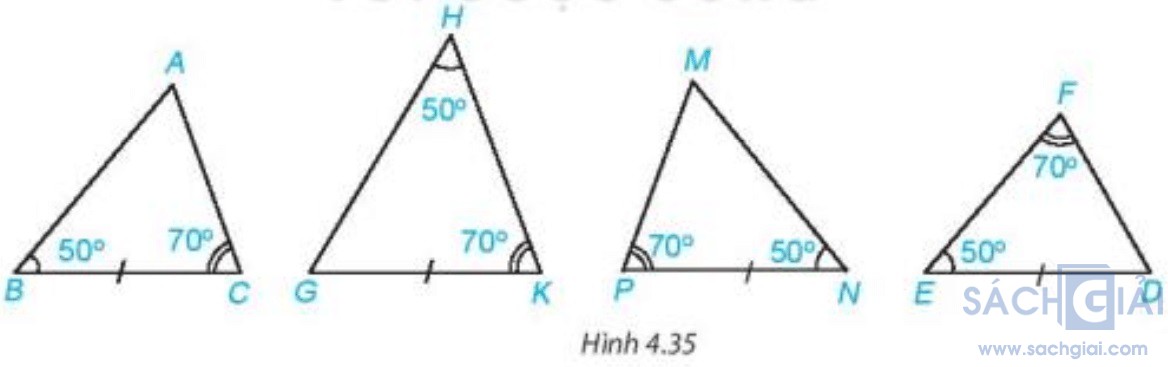
Câu hỏi trang 72: Hai tam giác nào trong Hình 4.35 bằng nhau?
Giải:
Tam giác GHK có góc H không phải góc kề của cạnh GK và tam giác DEF có góc F không phải góc kề của cạnh DE nên ta không xét hai tam giác này.
Xét hai tam giác ABC và MNP có:
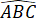 =
= 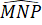 (cùng bằng 50o).
(cùng bằng 50o).
BC = NP (theo giả thiết).
 =
= 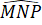 (cùng bằng 70o).
(cùng bằng 70o).
Vậy ΔABC = ΔMNP (g – c – g).
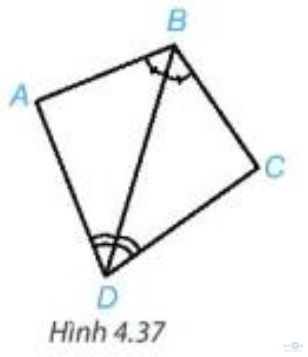
Luyện tập 2 - Trang 73: Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.
Giải:
Xét hai tam giác ABD và CBD có:
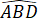 =
= 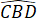 (theo giả thiết).
(theo giả thiết).
BD chung.
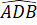 =
= 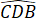 (theo giả thiết).
(theo giả thiết).
Vậy ΔABD = ΔCBD (g – c – g).
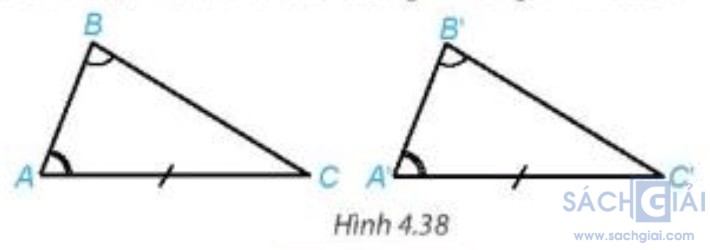
Thử thách nhỏ trang 73: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?
Giải:

Lấy giao điểm A của hai tia Bx và Cy, ta được tam giác ABC (H.4.33). Dùng thước thẳng có vạch chia đo độ dài hai cạnh AB, AC của tam giác ABC.

Giải:
Dùng thước thẳng có vạch chia, ta đo được độ dài cạnh AB xấp xỉ 2,2 cm và độ dài cạnh AC xấp xỉ 3,4 cm.
Hoạt động 4 - Trang 72: Vẽ thêm tam giác A′B′C′ sao cho B′C′= 3cm,
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác ABC và A′B′C′.
Hai tam giác ABC và A′B′C′ có bằng nhau không?

Giải:
Tương tự Hoạt động 3, ta vẽ hình như sau:
Bước 1. Vẽ đoạn thẳng B′C′ = 3cm
Bước 2. Dùng thước đo độ, vẽ hai tia
B′x′ và C′y′ sao cho
Bước 3. Lấy giao điểm A′ của hai tia B′x′ và C′y′ ta được tam giác A′B′C′
Vẽ thêm tam giác A'B'C' sao cho B'C'=3cm, góc A'B'C'=80 độ, góc A'C'B'=40 độ

- Dùng thước thẳng có vạch chia, ta đo được AB = A'B' ≈ 2,2 cm; AC = A'C' ≈ 3,4cm và BC = B'C' = 3cm.
- Xét hai tam giác ABC và A′B′C′ có:
AB = A′B′ (chứng minh trên).
BC = B'C' (chứng minh trên).
Vậy ΔABC = ΔA'B'C' (c – g – c).
Câu hỏi trang 72: Hai tam giác nào trong Hình 4.35 bằng nhau?

Giải:
Tam giác GHK có góc H không phải góc kề của cạnh GK và tam giác DEF có góc F không phải góc kề của cạnh DE nên ta không xét hai tam giác này.
Xét hai tam giác ABC và MNP có:
BC = NP (theo giả thiết).
Vậy ΔABC = ΔMNP (g – c – g).
Luyện tập 2 - Trang 73: Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau.

Giải:
Xét hai tam giác ABD và CBD có:
BD chung.
Vậy ΔABD = ΔCBD (g – c – g).
Thử thách nhỏ trang 73: Bạn Lan nói rằng: “Nếu tam giác này có một cạnh cùng một góc kề và góc đối diện tương ứng bằng một cạnh cùng một góc kề và góc đối diện của tam giác kia thì hai tam giác đó bằng nhau” (H.4.38). Theo em bạn Lan nói có đúng không? Vì sao?

Giải:

3. Giải bài tập trang 73
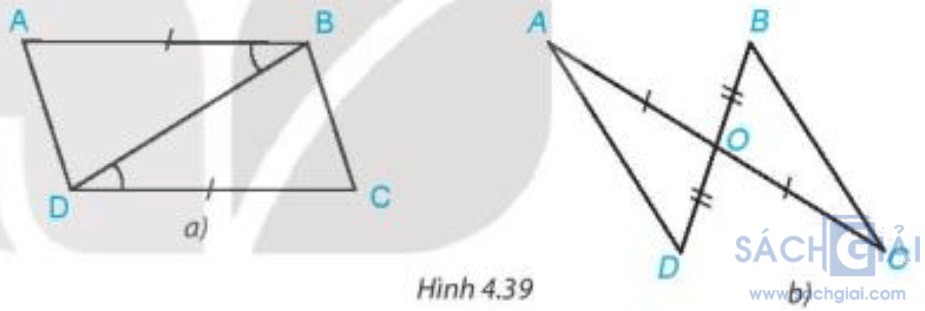
Bài 4.12 - Trang 73: Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Giải:
a) Xét Hình 4.39a.
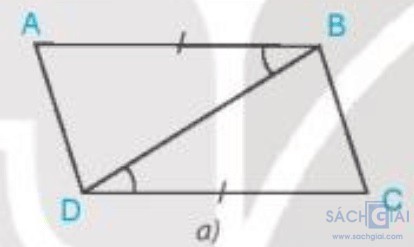
Xét tam giác ABD và tam giác CBD có:
AB = CD
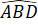 =
= 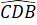
BD chung
Vậy ΔABD = ΔCBD(c.g.c)
b) Xét Hình 4.39b.
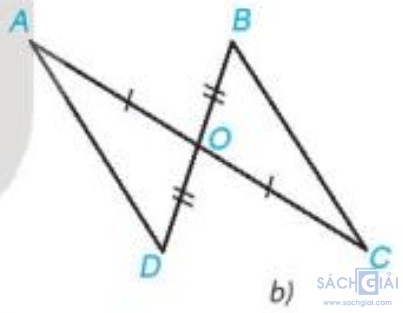
Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau
Xét hai tam giác OAD và OCB có:
AO = CO
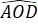 =
= 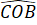 (đối đỉnh)
(đối đỉnh)
OD = OB
Vậy Δ OAD = Δ OCB(c.g.c)
Bài 4.13 - Trang 73: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.
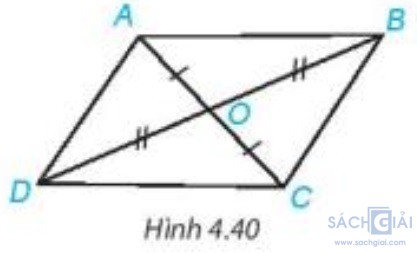
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;
b) Chứng minh rằng Δ DAB = Δ BCD.
Giải:
a) Hai cặp tam giác có chung đỉnh O bằng nhau là: AOB và COD; AOD và COB theo trường hợp cạnh – góc – cạnh.
b) Do hai tam giác AOD và COB nên: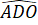 =
= 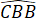 (2 góc tương ứng) và AD=BC (2 cạnh tương ứng)
(2 góc tương ứng) và AD=BC (2 cạnh tương ứng)
Xét ΔDAB và ΔBCD có:
AD = BC
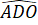 =
= 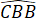
BD chung
Vậy ΔDAB = Δ BCD (c.g.c)
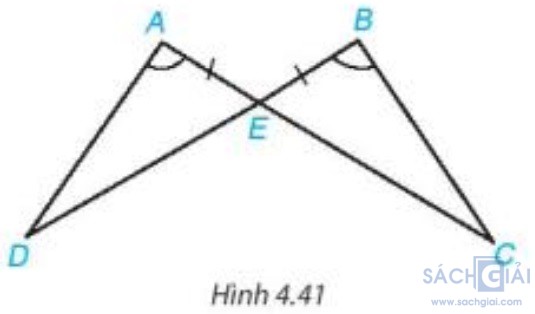
Bài 4.14 - Trang 73: Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
Giải:
Xét hai tam giác ADE và BCE có:
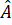 =
= 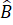
AE = BE
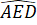 =
= 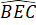 (đối đỉnh)
(đối đỉnh)
Vậy Δ ADE = Δ BCE(g.c.g)
Bài 4.15 - Trang 73: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:
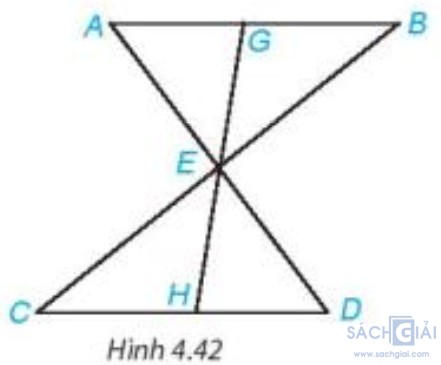
a) ΔBE = ΔDCE;
b) EG = EH.
Giải:



Giải:
a) Xét Hình 4.39a.

Xét tam giác ABD và tam giác CBD có:
AB = CD
BD chung
Vậy ΔABD = ΔCBD(c.g.c)
b) Xét Hình 4.39b.

Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau
Xét hai tam giác OAD và OCB có:
AO = CO
OD = OB
Vậy Δ OAD = Δ OCB(c.g.c)
Bài 4.13 - Trang 73: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;
b) Chứng minh rằng Δ DAB = Δ BCD.
Giải:
a) Hai cặp tam giác có chung đỉnh O bằng nhau là: AOB và COD; AOD và COB theo trường hợp cạnh – góc – cạnh.
b) Do hai tam giác AOD và COB nên:
Xét ΔDAB và ΔBCD có:
AD = BC
BD chung
Vậy ΔDAB = Δ BCD (c.g.c)
Bài 4.14 - Trang 73: Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.

Giải:
Xét hai tam giác ADE và BCE có:
AE = BE
Vậy Δ ADE = Δ BCE(g.c.g)
Bài 4.15 - Trang 73: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:

a) ΔBE = ΔDCE;
b) EG = EH.
Giải:


Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025