Giải SGK Toán 6 chương 3, bài 6: Hình có tâm đối xứng - Sách Cánh diều

Hoạt động 1 - Trang 111:
Giải:
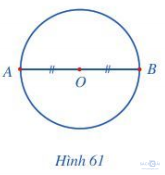
Quan sát đường kính AB của đường tròn tâm O (Hình 61)
Vì điểm O là trung điểm đoạn thẳng AB nên ta nói hai điểm A và B đối xứng với nhau qua tâm O.
Đường tròn tâm O là hình có tâm đối xứng và tâm đối xứng chính là tâm O của đường tròn.


Luyện tập 1 - Trang 112:
Giải:
Trong thực tế, có nhiều hình có tâm đối xứng. Chẳng hạn:
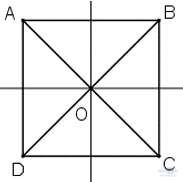
+) Hình vuông có tâm đối xứng là giao hai đường chéo (điểm O trong hình vẽ).

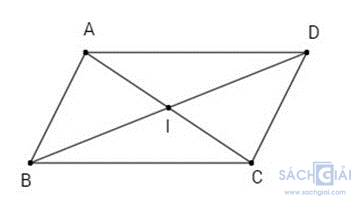
+) Hình bình hành có tâm đối xứng và tâm đối xứng của hình bình hành là giao điểm hai đường chéo của hình bình hành (điểm I trong hình vẽ).


Hoạt động 2 - Trang 111:
Giải:
Lấy bốn chiếc ê ke giống nhau để xếp thành hình như Hình 62.

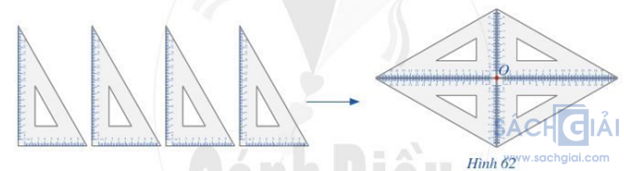
Hình 61 hay hình nhận được ở Hình 62 gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
 

Câu 1 - Trang 112: (Toán 6 tập 1 sách Cánh Diều) 
Trong các hình từ Hình 66 đến Hình 69, hình nào có tâm đối xứng? Nếu là hình có tâm đối xứng, hãy chỉ ra tâm đối xứng của hình đó.

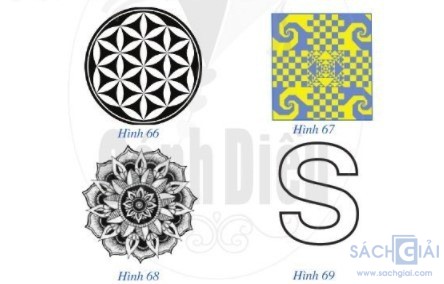
Giải:


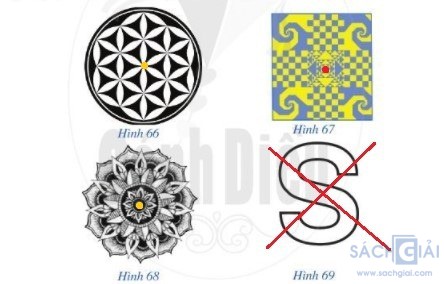
Câu 2 - Trang 112: (Toán 6 tập 1 sách Cánh Diều) 
Trong Hình 70, các hình từ a) đến c), hình nào có tâm đối xứng? Nếu là hình có tâm đối xứng, hãy chỉ ra trục đối xứng của hình đó ( kể cả màu sắc)

Giải:


Câu 3 - Trang 112: (Toán 6 tập 1 sách Cánh Diều) 
Hãy tìm một số hình có tâm đối xứng trong thực tiễn.
Giải:
Trong thực tiễn nhiều hình có tâm đối xứng, chẳng hạn:
+) Hình biển báo giao thông:


+) Hình bông hoa:

+) Hình viên gạch hoa: