Giải SGK Toán 6 chương 3, bài 3: Hình bình hành - Sách Cánh diều, trang 102, 103, 104.
Giải bài tập SGK Toán 6 chương 3, bài 3: Hình bình hành - Sách Cánh diều, trang 102, 103, 104.
Hoạt động 1 - Trang 102:
Dùng bốn chiếc que, trong đó hai que ngắn có độ dài bằng nhau, hai que dài có độ dài bằng nhau, để xếp thành hình bình hành như ở Hình 22.
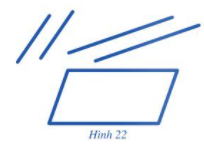
Giải:
Học sinh chuẩn bị que và thực hiện theo yêu cầu đề bài.
Luyện tập 1 - Trang 103:
Vẽ hai đoạn thẳng MN và MQ. Từ đó, vẽ hình bình hành MNPQ nhận hai đoạn thẳng MN và MQ làm cạnh.
Giải:
Ta lần lượt thực hiên qua các bước sau:
Bước 1. Lấy điểm M bất kì, vẽ hai đoạn thẳng MN, MQ sao cho MN và MQ không trùng lên nhau và có độ dài khác nhau như hình dưới đây.
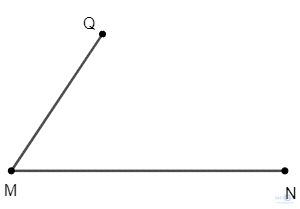
Bước 2. Lấy Q làm tâm, dùng compa vẽ một phần đường tròn có bán kính MN. Lấy N làm tâm, dùng compa vẽ một phần đường tròn có bán kính MQ. Gọi P là giao điểm của hai phần đường tròn này.
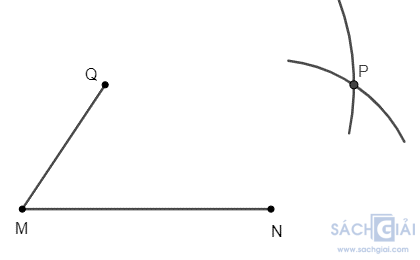
Bước 3. Dùng thước vẽ các đoạn thẳng QP và NP.
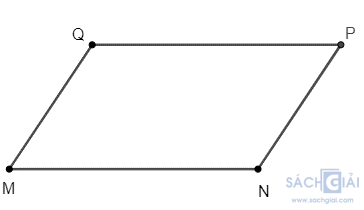
Khi đó ta được hình bình hành MNPQ.
Hoạt động 2 - Trang 102:
Với hình bình hành PQRS như ở Hình 23, thực hiện hoạt động sau:
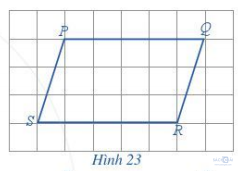
a) Quan sát xem các cặp cạnh đối PQ và RS; PS và QR có song song với nhau không.
b) Cắt hình bình hành PQRS theo đường chéo PR thành hai tam giác PQR (tô màu xanh) và tam giác RSP (tô màu hồng) (Hình 24 a, b). Dịch chuyển tam giác màu xanh cho trùng với tam giác màu hồng, trong đó đỉnh Q trùng với đỉnh S.
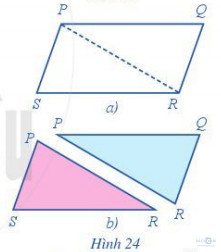
+ So sánh: cặp cạnh đối PQ và RS; cặp cạnh đối PS và QR.
+ So sánh góc PSR và góc PQR.
Giải:
a) Các cặp cạnh đối PQ và RS; PS và QR song song với nhau.
b) Các cặp cạnh đối PQ và RS; PS và QR bằng nhau.
Góc PSR và PQR bằng nhau.
Hoạt động 3 - Trang 102:
Cho trước hai đoạn thẳng AB, AD như Hình 26.
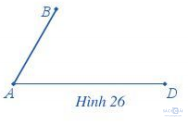
Vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.
Giải:
Ta có thể vẽ hình bình hành ABCD bằng thước và compa như sau:
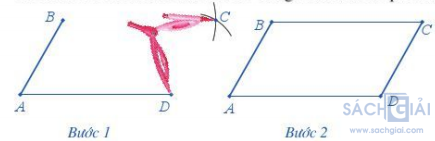
Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này.
Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.
Vậy ta được hình bình hành ABCD.
Hoạt động 4 - Trang 103:
Thực hiện các bước sau đây:
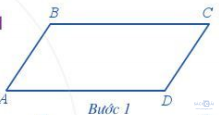
Bước 1. Vẽ hình bình hành ABCD
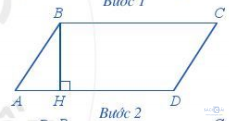
Bước 2. Vẽ BH vuông góc với AD
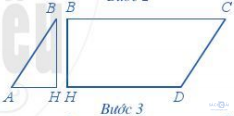
Bước 3. Cắt hình bình hành ABCD thành tam giác ABH và hình thang BCDH
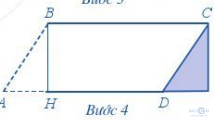
Bước 4. Ghép tam giác ABH vào hình thang BCDH để được hình chữ nhật
Bước 5. So sánh diện tích hình bình hành ABCD và diện tích hình chữ nhật được tạo thành ở Bước 4.
Giải:
Từ hình bình hành ta cắt rời thành 2 miếng bìa rồi ghép lại thành hình chữ nhật, nên hình chữ nhật được tạo thành từ các miếng bìa của hình bình hành. Do đó diện tích hình bình hành ABCD bằng diện tích hình chữ nhật được tạo thành.
Dùng bốn chiếc que, trong đó hai que ngắn có độ dài bằng nhau, hai que dài có độ dài bằng nhau, để xếp thành hình bình hành như ở Hình 22.

Giải:
Học sinh chuẩn bị que và thực hiện theo yêu cầu đề bài.
Luyện tập 1 - Trang 103:
Vẽ hai đoạn thẳng MN và MQ. Từ đó, vẽ hình bình hành MNPQ nhận hai đoạn thẳng MN và MQ làm cạnh.
Giải:
Ta lần lượt thực hiên qua các bước sau:
Bước 1. Lấy điểm M bất kì, vẽ hai đoạn thẳng MN, MQ sao cho MN và MQ không trùng lên nhau và có độ dài khác nhau như hình dưới đây.

Bước 2. Lấy Q làm tâm, dùng compa vẽ một phần đường tròn có bán kính MN. Lấy N làm tâm, dùng compa vẽ một phần đường tròn có bán kính MQ. Gọi P là giao điểm của hai phần đường tròn này.

Bước 3. Dùng thước vẽ các đoạn thẳng QP và NP.

Khi đó ta được hình bình hành MNPQ.
Hoạt động 2 - Trang 102:
Với hình bình hành PQRS như ở Hình 23, thực hiện hoạt động sau:

a) Quan sát xem các cặp cạnh đối PQ và RS; PS và QR có song song với nhau không.
b) Cắt hình bình hành PQRS theo đường chéo PR thành hai tam giác PQR (tô màu xanh) và tam giác RSP (tô màu hồng) (Hình 24 a, b). Dịch chuyển tam giác màu xanh cho trùng với tam giác màu hồng, trong đó đỉnh Q trùng với đỉnh S.

+ So sánh: cặp cạnh đối PQ và RS; cặp cạnh đối PS và QR.
+ So sánh góc PSR và góc PQR.
Giải:
a) Các cặp cạnh đối PQ và RS; PS và QR song song với nhau.
b) Các cặp cạnh đối PQ và RS; PS và QR bằng nhau.
Góc PSR và PQR bằng nhau.
Hoạt động 3 - Trang 102:
Cho trước hai đoạn thẳng AB, AD như Hình 26.

Vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.
Giải:
Ta có thể vẽ hình bình hành ABCD bằng thước và compa như sau:

Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này.
Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.
Vậy ta được hình bình hành ABCD.
Hoạt động 4 - Trang 103:
Thực hiện các bước sau đây:
Bước 1. Vẽ hình bình hành ABCD

Bước 2. Vẽ BH vuông góc với AD

Bước 3. Cắt hình bình hành ABCD thành tam giác ABH và hình thang BCDH

Bước 4. Ghép tam giác ABH vào hình thang BCDH để được hình chữ nhật
Bước 5. So sánh diện tích hình bình hành ABCD và diện tích hình chữ nhật được tạo thành ở Bước 4.

Giải:
Từ hình bình hành ta cắt rời thành 2 miếng bìa rồi ghép lại thành hình chữ nhật, nên hình chữ nhật được tạo thành từ các miếng bìa của hình bình hành. Do đó diện tích hình bình hành ABCD bằng diện tích hình chữ nhật được tạo thành.
* BÀI TẬP
Câu 1 - Trang 104: (Toán 6 tập 1 sách Cánh Diều)
Xem Hình 28 và cho biết hình nào trong số các hình đó là hình bình hành
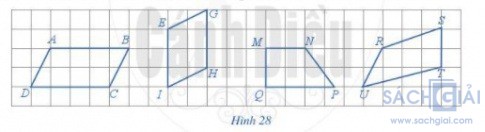
Giải:
Trong các hình trên: ABCD và EGHI là hình bình hành
Câu 2 - Trang 104: (Toán 6 tập 1 sách Cánh Diều)
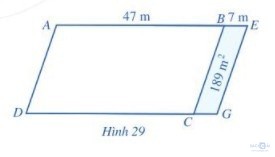
Một mảnh đất có dạng hình bình hành ABCD với AB = 47 m. Người ta mở rộng mảnh đất này thành hình bình hành AEGD có diện tích lớn hơn diện tích mảnh đất ban đầu là 189 m2 và BE = 7m ( Hình 29). Tính diện tích mảnh đất ban đầu.
Giải:
Chiều cao của hình bình hành là: 189 : 7 = 27 m
Diện tích mảnh đất ban đầu là: 47 x 27 = 1269 (m2)
Câu 3 - Trang 104: (Toán 6 tập 1 sách Cánh Diều)
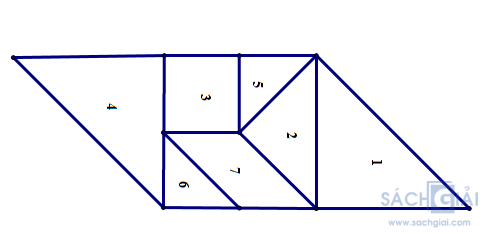
Sử dụng các mảnh bìa như Hình 21 để ghép thành một hình bình hành.
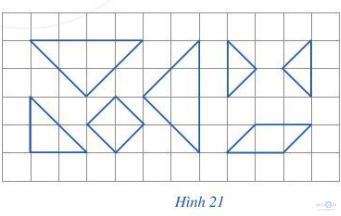
Giải:
Ta đặt tên các mảnh như sau:
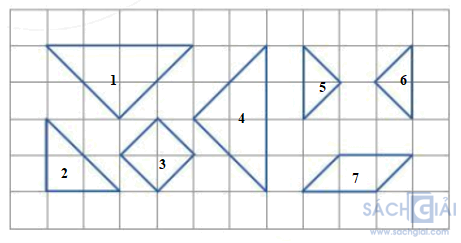
Ta ghép thành hình bình hành:
Xem Hình 28 và cho biết hình nào trong số các hình đó là hình bình hành

Giải:
Trong các hình trên: ABCD và EGHI là hình bình hành
Câu 2 - Trang 104: (Toán 6 tập 1 sách Cánh Diều)

Một mảnh đất có dạng hình bình hành ABCD với AB = 47 m. Người ta mở rộng mảnh đất này thành hình bình hành AEGD có diện tích lớn hơn diện tích mảnh đất ban đầu là 189 m2 và BE = 7m ( Hình 29). Tính diện tích mảnh đất ban đầu.
Giải:
Chiều cao của hình bình hành là: 189 : 7 = 27 m
Diện tích mảnh đất ban đầu là: 47 x 27 = 1269 (m2)
Câu 3 - Trang 104: (Toán 6 tập 1 sách Cánh Diều)
Sử dụng các mảnh bìa như Hình 21 để ghép thành một hình bình hành.

Giải:
Ta đặt tên các mảnh như sau:

Ta ghép thành hình bình hành:

Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
 Giải SGK Toán 6 chương 3, bài 4: Hình thang cân - Sách Cánh diều
Giải SGK Toán 6 chương 3, bài 4: Hình thang cân - Sách Cánh diều