Giải SGK Toán 6 chương 1, bài 9: Dấu hiệu chia hết cho 3, cho 9 - Sách Cánh diều
Giải bài tập SGK Toán 6 chương 1, bài 9: Dấu hiệu chia hết cho 3, cho 9 - Sách Cánh diều, trang 35, 36, 37.
Trong giờ học Lịch sử, cô hạnh nêu một năm của thế kỉ XX đánh dấu một mốc quan trọng trong lịch sử đất nước ta. Năm đó là số được viết từ các chữ số lẻ khác nhau. Số đó còn chia hết cho 5 và chia cho 9 dư 4.
Trong giờ học Lịch sử, cô hạnh nêu một năm của thế kỉ XX đánh dấu một mốc quan trọng
Hỏi năm đó là năm nào?
Giải:
Ta giải quyết bài tập này sau khi học xong bài "Dấu hiệu chia hết cho 3, cho 9".
Theo đề bài ta thấy năm cần tìm thuộc thế kỉ XX, mà thế kỷ XX là khoảng thời gian tính từ thời điểm năm 1901 đến hết năm 2000 (bằng 100 năm).
Mà năm cần tìm được viết từ các chữ số lẻ khác nhau nên nó có dạng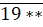 (với * là các số tự nhiên lẻ từ 3 đến 7)
(với * là các số tự nhiên lẻ từ 3 đến 7)
Ta có: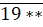 chia hết cho 5 nên nó phải có chữ số tận cùng là 0 hoặc 5, nhưng số đó được viết từ các chữ số lẻ khác nhau nên chữ số tận cùng của
chia hết cho 5 nên nó phải có chữ số tận cùng là 0 hoặc 5, nhưng số đó được viết từ các chữ số lẻ khác nhau nên chữ số tận cùng của 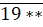 phải là 5.
phải là 5.
Khi đó số cần tìm có dạng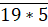
Các chữ số lẻ còn lại thỏa mãn * là 3, 7
TH1. * = 3 khi đó ta có số 1935 với 1 + 9 + 3 + 5 = 18 chia hết cho 9. Hay 1935 chia hết cho 9 (không thỏa mãn)
TH2. * = 7 khi đó ta có số 1975 với 1 + 9 + 7 + 5 = 22 không chia hết cho 9, mà 22 chia 9 dư 4 nên 1975 chia cho 9 dư 4.
Vậy năm cần tìm là năm 1975.
Trong giờ học Lịch sử, cô hạnh nêu một năm của thế kỉ XX đánh dấu một mốc quan trọng
Hỏi năm đó là năm nào?
Giải:
Ta giải quyết bài tập này sau khi học xong bài "Dấu hiệu chia hết cho 3, cho 9".
Theo đề bài ta thấy năm cần tìm thuộc thế kỉ XX, mà thế kỷ XX là khoảng thời gian tính từ thời điểm năm 1901 đến hết năm 2000 (bằng 100 năm).
Mà năm cần tìm được viết từ các chữ số lẻ khác nhau nên nó có dạng
Ta có:
Khi đó số cần tìm có dạng
Các chữ số lẻ còn lại thỏa mãn * là 3, 7
TH1. * = 3 khi đó ta có số 1935 với 1 + 9 + 3 + 5 = 18 chia hết cho 9. Hay 1935 chia hết cho 9 (không thỏa mãn)
TH2. * = 7 khi đó ta có số 1975 với 1 + 9 + 7 + 5 = 22 không chia hết cho 9, mà 22 chia 9 dư 4 nên 1975 chia cho 9 dư 4.
Vậy năm cần tìm là năm 1975.
I. Dấu hiệu chia hết cho 3
Hoạt động 1 - Trang 38:
a) Thực hiện phép tính 123 : 3 và nêu quan hệ chia hết của 123 với 3
b) Tìm tổng S các chữ số của 123 và nêu quan hệ chia hết của S với 3
Giải:
a) 123 : 3 = 41 => Số 123 chia hết cho 3
b) Tổng các chữ số của số 123: S = 1 + 2 + 3 = 6 => S chia hết cho 3
Luyện tập 1 - Trang 38:
Viết một số có hai chữ số sao cho
a) Số có hai chữ số chia hết cho 3 và 5
b) Số chia hết cho cả ba số 2, 3, 5
Giải:
a) Số có hai chữ số chia hết cho 3 và 5 là: 15
b) Số chia hết cho cả ba số 2, 3, 5 là 60.
a) Thực hiện phép tính 123 : 3 và nêu quan hệ chia hết của 123 với 3
b) Tìm tổng S các chữ số của 123 và nêu quan hệ chia hết của S với 3
Giải:
a) 123 : 3 = 41 => Số 123 chia hết cho 3
b) Tổng các chữ số của số 123: S = 1 + 2 + 3 = 6 => S chia hết cho 3
Luyện tập 1 - Trang 38:
Viết một số có hai chữ số sao cho
a) Số có hai chữ số chia hết cho 3 và 5
b) Số chia hết cho cả ba số 2, 3, 5
Giải:
a) Số có hai chữ số chia hết cho 3 và 5 là: 15
b) Số chia hết cho cả ba số 2, 3, 5 là 60.
II. Dấu hiệu chia hết cho 9
Hoạt động 2 - Trang 39:
a) Thực hiện phép tính 135 : 9 và nêu quan hệ chia hết của 135 với 9
b) Tìm tổng S các chữ số của 135 và nêu quan hệ chia hết của S với 9
Giải:
a) 135 : 9 = 15 => 135 chia hết cho 9
b) S = 1 + 3 + 5 = 9 => S chia hết cho 9
Luyện tập 2 - Trang 39:
Viết một số có hai chữ số sao cho
a) Số có hai chữ số chia hết cho 2 và 9
b) Số có hai chữ số chia hết cho cả ba số 2, 5, 9
Giải:
a) Số có hai chữ số chia hết cho 2 và 9 là: 36
b) Số có hai chữ số chia hết cho cả ba số 2, 5, 9 là: 90
a) Thực hiện phép tính 135 : 9 và nêu quan hệ chia hết của 135 với 9
b) Tìm tổng S các chữ số của 135 và nêu quan hệ chia hết của S với 9
Giải:
a) 135 : 9 = 15 => 135 chia hết cho 9
b) S = 1 + 3 + 5 = 9 => S chia hết cho 9
Luyện tập 2 - Trang 39:
Viết một số có hai chữ số sao cho
a) Số có hai chữ số chia hết cho 2 và 9
b) Số có hai chữ số chia hết cho cả ba số 2, 5, 9
Giải:
a) Số có hai chữ số chia hết cho 2 và 9 là: 36
b) Số có hai chữ số chia hết cho cả ba số 2, 5, 9 là: 90
* Bài tập
Câu 1 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Cho các số 104, 627, 3 114, 5 123,6 831 và 72 102. Trong các số đó:
a) Số nào chia hết cho 3? Vì sao?
b) Số nào không chia hết cho 3? Vì sao?
c) Số nào chia hết cho 9? Vì sao?
d) Số nào chia hết cho 3, nhưng không chia hết cho 9? Vì sao?
Giải:
Ta áp dụng dấu hiệu chia hết cho 3 và dấu hiệu chia hết cho 9 để thực hiện bài tập này.
a) Trong các số đã cho ta có:
+ Số 627 chia hết cho 3 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3.
+ Số 3 114 chia hết cho 3 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 3.
+ Số 6 831 chia hết cho 3 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 3.
+ Số 72 102 chia hết cho 3 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3.
b) Ta có:
+ Số 104 không chia hết cho 3 vì tổng các chữ số 1 + 0 + 4 = 5 không chia hết cho 3.
+ Số 5 123 không chia hết cho 3 vì tổng các chữ số 5 + 1 + 2 + 3 = 11 không chia hết cho 3.
c) Ta có:
+ Số 3 114 chia hết cho 9 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 9.
+ Số 6 831 chia hết cho 9 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 9.
d) Ta có:
+ Số 627 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3 nhưng không chia hết cho 9.
+ Số 72 102 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3 nhưng không chia hết cho 9.
Câu 2 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Trong các số 2, 3, 5, 9 số nào là ước của n với
a) n = 4 536;
b) n = 3 240;
c) n = 9 805?
Giải:
a) n = 4 536
+ Vì số 4 536 có chữ số tận cùng là 6 nên số này chia hết cho 2 và không chia hết cho 5.
+ Số 4 536 có tổng các chữ số là 4 + 5 + 3 + 6 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 4 536 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 4 536 là 2; 3; 9.
b) n = 3 240
+ Số 3 240 có chữ số tận cùng là 0 nên số này chia hết cho cả 2 và 5.
+ Số 3 240 có tổng các chữ số là 3 + 2 + 4 + 0 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 3 240 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 3 240 là 2; 3; 5; 9.
c) n = 9 805
+ Số 9 805 có chữ số tận cùng là 5 nên số này chia hết cho 5 và không chia hết cho 2.
+ Số 9 805 có tổng các chữ số là 9 + 8 + 0 + 5 = 22 không chia hết cho cả 3 và 9 nên số 9 805 không chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 9 805 là 5.
Câu 3 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Tìm chữ số thích hợp ở dấu * để số:
a) chia hết cho 3;
chia hết cho 3;
b)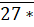 chia hết cho 9
chia hết cho 9
Giải:
a) Vì * là một chữ số trong số nên * phải là một trong các số: 0; 1; 2; …; 9.
nên * phải là một trong các số: 0; 1; 2; …; 9.
Số chia hết cho 3 chia hết cho 3 nên tổng các chữ số của số
chia hết cho 3 chia hết cho 3 nên tổng các chữ số của số  hia hết cho 3 là (3 + * + 7) = (10 + *) phải là số chia hết cho 3.
hia hết cho 3 là (3 + * + 7) = (10 + *) phải là số chia hết cho 3.
Thử thay * lần lượt bằng các số 0; 1; 2; …; 9, ta thấy các số thỏa mãn là 2; 5; 8.
Vậy các chữ số thích hợp điền vào dấu * để số chia hết cho 3 chia hết cho 3 là: 2; 5; 8.
chia hết cho 3 chia hết cho 3 là: 2; 5; 8.
b) Vì * là một chữ số trong số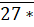 chia hết cho 3 nên * phải là một trong các số: 0; 1; 2; …; 9.
chia hết cho 3 nên * phải là một trong các số: 0; 1; 2; …; 9.
Số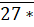 chia hết cho 3 chia hết cho 9 nên tổng các chữ số của số Tìm chữ số thích hợp ở dấu * để số: a) 3*7 chia hết cho 3 là (2 + 7 + *) = (9 + *) phải là số chia hết cho 9.
chia hết cho 3 chia hết cho 9 nên tổng các chữ số của số Tìm chữ số thích hợp ở dấu * để số: a) 3*7 chia hết cho 3 là (2 + 7 + *) = (9 + *) phải là số chia hết cho 9.
Thử thay * lần lượt bằng các số 0; 1; 2; …; 9, ta thấy các số thỏa mãn là 0; 9.
Vậy các chữ số thích hợp điền vào dấu * để số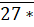 chia hết cho 3 chia hết cho 9 là: 0; 9.
chia hết cho 3 chia hết cho 9 là: 0; 9.
Câu 4 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Tìm chữ số thích hợp ở dấu * để số:
a)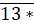 chia hết cho 5 và 9;
chia hết cho 5 và 9;
b)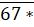 chia hết cho 2 và 3.
chia hết cho 2 và 3.
Giải:
a) Vì * là một chữ số trong số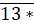 chia hết cho 5 và 9 nên * phải là một trong các số: 0; 1; 2; …; 9.
chia hết cho 5 và 9 nên * phải là một trong các số: 0; 1; 2; …; 9.
Số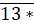 chia hết cho 5 và 9 chia hết cho 5 nên
chia hết cho 5 và 9 chia hết cho 5 nên 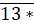 chia hết cho 5 và 9 phải có chữ số tận cùng là 0 hoặc 5, hay * phải là 0 hoặc 5.
chia hết cho 5 và 9 phải có chữ số tận cùng là 0 hoặc 5, hay * phải là 0 hoặc 5.
Số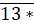 chia hết cho 5 và 9 chia hết cho 9 nên tổng các chữ số của số
chia hết cho 5 và 9 chia hết cho 9 nên tổng các chữ số của số 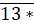 chia hết cho 5 và 9 là (1 + 3 + *) = (4 + *) phải là số chia hết cho 9.
chia hết cho 5 và 9 là (1 + 3 + *) = (4 + *) phải là số chia hết cho 9.
Thay * lần lượt bằng các số 0; 5 ta được:
4 + 0 = 5 không chia hết cho 9
4 + 5 = 9 chia hết cho 9
Vậy chữ số thích hợp điền vào dấu * để số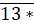 chia hết cho 5 và 9 chia hết cho cả 5 và 9 là: 5 hay * = 5.
chia hết cho 5 và 9 chia hết cho cả 5 và 9 là: 5 hay * = 5.
b) Số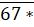 chia hết cho 2 nên
chia hết cho 2 nên 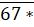 phải có chữ số tận cùng là 0; 2; 4; 6; 8, hay * phải là một trong các số: 0; 2; 4; 6; 8.
phải có chữ số tận cùng là 0; 2; 4; 6; 8, hay * phải là một trong các số: 0; 2; 4; 6; 8.
Số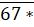 chia hết cho 3 nên tổng các chữ số của số
chia hết cho 3 nên tổng các chữ số của số 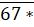 là (6 + 7 + *) = (13 + *) phải là số chia hết cho 3.
là (6 + 7 + *) = (13 + *) phải là số chia hết cho 3.
Thay * lần lượt bằng các số 0; 2; 4; 6; 8 ta được:
13 + 0 = 13 không chia hết cho 3
13 + 2 = 15 chia hết cho 3
13 + 4 = 17 không chia hết cho 3
13 + 6 = 19 không chia hết cho 3
13 + 8 = 21 chia hết cho 3
Vậy các chữ số thích hợp điền vào dấu * để số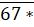 chia hết cho cả 2 và 3 là: 2; 8 hay * = 2 hoặc * = 8.
chia hết cho cả 2 và 3 là: 2; 8 hay * = 2 hoặc * = 8.
Câu 5 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Các lớp 6A, 6B, 6C, 6D, 6E có số học sinh tương ứng là 40, 45, 39, 44, 42. Hỏi:
a) Lớp nào có thể xếp thành 3 hàng với số học sinh ở mỗi hàng là như nhau?
b) Lớp nào có thể xếp thành 9 hàng với số học sinh ở mỗi hàng là như nhau?
c) Có thể xếp tất cả học sinh của năm lớp đó thành 3 hàng với số học sinh ở mỗi hàng là như nhau được không?
d) Có thể xếp tất cả học sinh của năm lớp đó thành 9 hàng với số học sinh ở mỗi hàng là như nhau được không?
Giải:
a) Để số học sinh của một lớp có thể xếp thành ba hàng với số học sinh ở mỗi hàng là như nhau thì tổng số học sinh của lớp đó phải là số chia hết cho 3.
Trong các số 40; 45; 39; 44; 42 thì:
+ Số 45 chia hết cho 3 (vì 45 có tổng các chữ số là 4 + 5 = 9 chia hết cho 3)
+ Số 39 chia hết cho 3 (vì 39 có tổng các chữ số là 3 + 9 = 12 chia hết cho 3)
+ Số 42 chia hết cho 3 (vì 42 có tổng các chữ số là 4 + 2 = 6 chia hết cho 3)
Vậy các lớp 6B, 6C; 6E có thể xếp thành 3 hàng với số học sinh ở mỗi hàng là như nhau.
b) Để số học sinh của một lớp có thể xếp thành chín hàng với số học sinh ở mỗi hàng là như nhau thì tổng số học sinh của lớp đó phải là số chia hết cho 9.
Trong các số 40; 45; 39; 44; 42 thì chỉ có số 45 chia hết cho 9 (vì 45 có tổng các chữ số là 4 + 5 = 9 chia hết cho 9).
Vậy chỉ có lớp 6B có thể xếp thành 9 hàng với số học sinh ở mỗi hàng là như nhau.
c) Tổng số học sinh của cả 5 lớp 6A, 6B, 6C, 6D, 6E là:
40 + 45 + 39 + 44 + 42 = 210 (học sinh)
Ta có số 210 là số chia hết cho 3 (vì tổng các chữ số của số 210 là 2 + 1 + 0 = 3 chia hết cho 3)
Do đó tổng số học sinh của cả 5 lớp là số chia hết cho 3.
Vậy ta có thể xếp tất cả học sinh của 5 lớp đó thành 3 hàng với số học sinh ở mỗi hàng là như nhau.
d) Ta có số 210 là số không chia hết cho 9 (vì tổng các chữ số của số 210 là 2 + 1 + 0 = 3 không chia hết cho 9)
Do đó tổng số học sinh của cả 5 lớp là số không chia hết cho 9.
Vậy ta không thể xếp tất cả học sinh của 5 lớp đó thành 9 hàng với số học sinh ở mỗi hàng là như nhau.
Cho các số 104, 627, 3 114, 5 123,6 831 và 72 102. Trong các số đó:
a) Số nào chia hết cho 3? Vì sao?
b) Số nào không chia hết cho 3? Vì sao?
c) Số nào chia hết cho 9? Vì sao?
d) Số nào chia hết cho 3, nhưng không chia hết cho 9? Vì sao?
Giải:
Ta áp dụng dấu hiệu chia hết cho 3 và dấu hiệu chia hết cho 9 để thực hiện bài tập này.
a) Trong các số đã cho ta có:
+ Số 627 chia hết cho 3 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3.
+ Số 3 114 chia hết cho 3 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 3.
+ Số 6 831 chia hết cho 3 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 3.
+ Số 72 102 chia hết cho 3 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3.
b) Ta có:
+ Số 104 không chia hết cho 3 vì tổng các chữ số 1 + 0 + 4 = 5 không chia hết cho 3.
+ Số 5 123 không chia hết cho 3 vì tổng các chữ số 5 + 1 + 2 + 3 = 11 không chia hết cho 3.
c) Ta có:
+ Số 3 114 chia hết cho 9 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 9.
+ Số 6 831 chia hết cho 9 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 9.
d) Ta có:
+ Số 627 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3 nhưng không chia hết cho 9.
+ Số 72 102 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3 nhưng không chia hết cho 9.
Câu 2 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Trong các số 2, 3, 5, 9 số nào là ước của n với
a) n = 4 536;
b) n = 3 240;
c) n = 9 805?
Giải:
a) n = 4 536
+ Vì số 4 536 có chữ số tận cùng là 6 nên số này chia hết cho 2 và không chia hết cho 5.
+ Số 4 536 có tổng các chữ số là 4 + 5 + 3 + 6 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 4 536 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 4 536 là 2; 3; 9.
b) n = 3 240
+ Số 3 240 có chữ số tận cùng là 0 nên số này chia hết cho cả 2 và 5.
+ Số 3 240 có tổng các chữ số là 3 + 2 + 4 + 0 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 3 240 là số chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 3 240 là 2; 3; 5; 9.
c) n = 9 805
+ Số 9 805 có chữ số tận cùng là 5 nên số này chia hết cho 5 và không chia hết cho 2.
+ Số 9 805 có tổng các chữ số là 9 + 8 + 0 + 5 = 22 không chia hết cho cả 3 và 9 nên số 9 805 không chia hết cho cả 3 và 9.
Do đó trong các số 2; 3; 5; 9, các ước số của số n = 9 805 là 5.
Câu 3 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Tìm chữ số thích hợp ở dấu * để số:
a)
b)
Giải:
a) Vì * là một chữ số trong số
Số
Thử thay * lần lượt bằng các số 0; 1; 2; …; 9, ta thấy các số thỏa mãn là 2; 5; 8.
Vậy các chữ số thích hợp điền vào dấu * để số
b) Vì * là một chữ số trong số
Số
Thử thay * lần lượt bằng các số 0; 1; 2; …; 9, ta thấy các số thỏa mãn là 0; 9.
Vậy các chữ số thích hợp điền vào dấu * để số
Câu 4 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Tìm chữ số thích hợp ở dấu * để số:
a)
b)
Giải:
a) Vì * là một chữ số trong số
Số
Số
Thay * lần lượt bằng các số 0; 5 ta được:
4 + 0 = 5 không chia hết cho 9
4 + 5 = 9 chia hết cho 9
Vậy chữ số thích hợp điền vào dấu * để số
b) Số
Số
Thay * lần lượt bằng các số 0; 2; 4; 6; 8 ta được:
13 + 0 = 13 không chia hết cho 3
13 + 2 = 15 chia hết cho 3
13 + 4 = 17 không chia hết cho 3
13 + 6 = 19 không chia hết cho 3
13 + 8 = 21 chia hết cho 3
Vậy các chữ số thích hợp điền vào dấu * để số
Câu 5 - Trang 39: (Toán 6 tập 1 sách Cánh Diều)
Các lớp 6A, 6B, 6C, 6D, 6E có số học sinh tương ứng là 40, 45, 39, 44, 42. Hỏi:
a) Lớp nào có thể xếp thành 3 hàng với số học sinh ở mỗi hàng là như nhau?
b) Lớp nào có thể xếp thành 9 hàng với số học sinh ở mỗi hàng là như nhau?
c) Có thể xếp tất cả học sinh của năm lớp đó thành 3 hàng với số học sinh ở mỗi hàng là như nhau được không?
d) Có thể xếp tất cả học sinh của năm lớp đó thành 9 hàng với số học sinh ở mỗi hàng là như nhau được không?
Giải:
a) Để số học sinh của một lớp có thể xếp thành ba hàng với số học sinh ở mỗi hàng là như nhau thì tổng số học sinh của lớp đó phải là số chia hết cho 3.
Trong các số 40; 45; 39; 44; 42 thì:
+ Số 45 chia hết cho 3 (vì 45 có tổng các chữ số là 4 + 5 = 9 chia hết cho 3)
+ Số 39 chia hết cho 3 (vì 39 có tổng các chữ số là 3 + 9 = 12 chia hết cho 3)
+ Số 42 chia hết cho 3 (vì 42 có tổng các chữ số là 4 + 2 = 6 chia hết cho 3)
Vậy các lớp 6B, 6C; 6E có thể xếp thành 3 hàng với số học sinh ở mỗi hàng là như nhau.
b) Để số học sinh của một lớp có thể xếp thành chín hàng với số học sinh ở mỗi hàng là như nhau thì tổng số học sinh của lớp đó phải là số chia hết cho 9.
Trong các số 40; 45; 39; 44; 42 thì chỉ có số 45 chia hết cho 9 (vì 45 có tổng các chữ số là 4 + 5 = 9 chia hết cho 9).
Vậy chỉ có lớp 6B có thể xếp thành 9 hàng với số học sinh ở mỗi hàng là như nhau.
c) Tổng số học sinh của cả 5 lớp 6A, 6B, 6C, 6D, 6E là:
40 + 45 + 39 + 44 + 42 = 210 (học sinh)
Ta có số 210 là số chia hết cho 3 (vì tổng các chữ số của số 210 là 2 + 1 + 0 = 3 chia hết cho 3)
Do đó tổng số học sinh của cả 5 lớp là số chia hết cho 3.
Vậy ta có thể xếp tất cả học sinh của 5 lớp đó thành 3 hàng với số học sinh ở mỗi hàng là như nhau.
d) Ta có số 210 là số không chia hết cho 9 (vì tổng các chữ số của số 210 là 2 + 1 + 0 = 3 không chia hết cho 9)
Do đó tổng số học sinh của cả 5 lớp là số không chia hết cho 9.
Vậy ta không thể xếp tất cả học sinh của 5 lớp đó thành 9 hàng với số học sinh ở mỗi hàng là như nhau.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
 Giải SGK Toán 6 chương 1, bài 10: Số nguyên tố. Hợp số - Sách Cánh diều
Giải SGK Toán 6 chương 1, bài 10: Số nguyên tố. Hợp số - Sách Cánh diều