Giải SGK Toán 6 chương 1, bài 11: Phân tích một số ra thừa số nguyên tố - Sách Cánh diều
Giải bài tập SGK Toán 6 chương 1, bài 11: Phân tích một số ra thừa số nguyên tố - Sách Cánh diều, trang 35, 36, 37.
I. Cách tìm một ước nguyên tố của một số
Hoạt động 1 - Trang 44:a) Nêu các số nguyên tố nhỏ hơn 30
b) Tìm một ước nguyên tố của 91
Giải:
a) Các số nguyên tố nhỏ hơn 30 là: 2; 3; 5; 7; 9; 11; 13; 17; 19; 23; 29
b) Một ước số nguyên tố của 91 là: 7
Luyện tập 1 - Trang 44:
Tìm một ước nguyên tố của 187
Giải:
Một ước nguyên tố của 187 là: 11
II. Phân tích một số ra thừa số nguyên tố
Luyện tập 2 - Trang 45Phân tích số 40 ra thừa số nguyên tố bằng cách viết rẽ nhánh và theo chiều dọc
Giải:
Cách viết rẽ nhánh
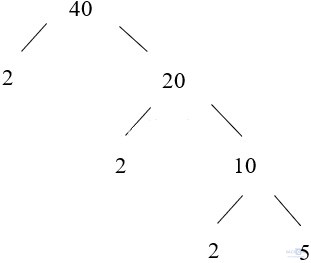
Theo chiều dọc

Luyện tập 3 - Trang 45:
Phân tích số 450 ra thừa số nguyên tố
Giải:
Cách 1: Ta có: 450 = 10 . 45
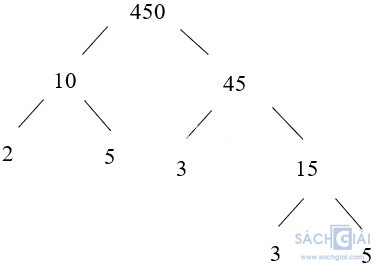
Vậy 450 = 2 . 5 . 3 . 3 . 5 = 2 . 32 . 52.
Cách 2: Ta có: 450 = 9 . 50
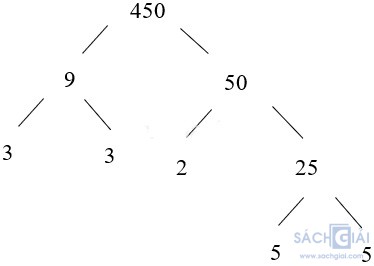
Vậy 450 = 3 . 3 . 2 . 5 . 5 = 2 . 32 . 52.
Cách 3. Ta phân tích "theo cột dọc".
| 450 225 75 25 5 |
2 3 3 5 5 |
| 1 |
Vậy ta 450 = 2 . 3 . 3 . 5 . 5 = 2 . 32 . 52.
* Bài tập
Câu 1 - Trang 46: (Toán 6 tập 1 sách Cánh Diều)Phân tích các số nguyên ra thừa số nguyên tố: 45, 78, 270, 299
Giải:
Phân tích số 45 bằng cách viết "theo cột dọc"
| 45 15 5 1 |
3 3 5 |
Vậy 45 = 3 . 3. 5 = 32 . 5.
- Phân tích số 78 bằng cách viết "theo cột dọc":
| 78 39 13 1 |
2 3 13 |
Vậy 78 = 2 . 3. 13.
- Phân tích số 270 bằng cách viết "rẽ nhánh":
Ta có: 270 = 10 . 27
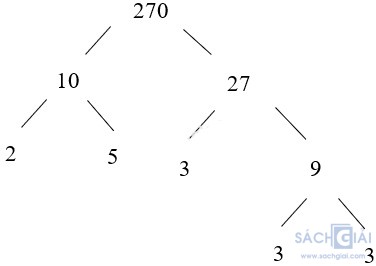
Vậy 270 = 2 . 5 . 3 . 3. 3 = 2 . 33 . 5.
- Phân tích số 299
Vậy 299 = 13 . 23.
Câu 2 - Trang 46: (Toán 6 tập 1 sách Cánh Diều)
a) Biết 400= 24.52. Hãy viết 800 thành tích các thừa số nguyên tố
b) Biết 320= 26.5. Hãy viết 3200 thành tích các thừa số nguyên tố
Giải:
a) Ta có: 800 = 2 . 400
Mà 400 =24.52
Do đó: 800 = 2 . (24.52) = (21.24). 52 = 24 + 1. 52 = 25 . 52
Vậy 800 = 25 . 52.
b) Ta có: 3 200 = 10 . 320
Mà 10 = 2 . 5 và 320 = 26 . 5
Do đó: 3 200 = (2 . 5) . (26 . 5) = (21 . 26) . (5 . 5) = 21 + 6 . 52 = 27 . 52
Vậy 3 200 = 27 . 52
Câu 3 - Trang 46: (Toán 6 tập 1 sách Cánh Diều)
a) Biết 2700= 22.33.52. Hãy viết 270 và 900 thành tích các thừa số nguyên tố
b) Biết 3600= 24.32.52. Hãy viết 180 và 600 thành tích các thừa số nguyên tố
Giải:
a) Ta có: 2 700 = 10 . 270 = 3 . 900
Mà 10 = 2 . 5 và 2 700 = 22 . 33 . 52
Do đó: 270 = 2 700 : 10 = (22 . 33 . 52 ) : (2 . 5) = (22 : 2) . 33 . (52 : 5) = 2 . 33 . 5
900 = 2 700 : 3 = (22 . 33 . 52 ) : 3 = 22 . (33 : 3) . 52 = 22 . 32 . 52
Vậy 270 = 2 . 33 . 5 và 900 = 22 . 32 . 52
b) Ta có: 3 600 = 20 . 180 = 6 . 600
Mà 20 = 2 . 10 = 2 . 2 . 5 = 22 . 5; 6 = 2 . 3 và 3 600 = 24 . 32 . 52
Do đó: 180 = 3 600 : 20 = (24 . 32 . 52) : (22 . 5) = (24 : 22) . 32 .(52 : 5)
= 24-2 . 32 . 5 = 22 . 32 . 5
600 = 3 600 : 6 = (24 . 32 . 52) : (2 . 3) = (24 : 2) . (32: 3) . 52 = 24-1 . 3 . 52 = 23 . 3 . 52
Vậy 180 = 22 . 32 . 5 và 600 = 23 . 3 . 52
Câu 4 - Trang 46: (Toán 6 tập 1 sách Cánh Diều)
Hãy chỉ ra 2 số tự nhiên mà mỗi số đó có đúng 3 ước nguyên tố
Giải:
Ta lấy tích của ba số nguyên tố khác nhau bất kì, ta được số tự nhiên có đúng ba ước nguyên tố.
Ví dụ: 2 . 3. 5 = 30; 3 . 5 . 7 = 105; 5. 7 . 11 = 385; …
Vậy hai số tự nhiên mà mỗi số có đúng 3 ước nguyên tố là: 30; 105.
(Tương tự cách làm trên, các em có thể chọn hai số khác thỏa mãn yêu cầu).
Câu 5 - Trang 46: (Toán 6 tập 1 sách Cánh Diều)
Phân tích số 84 ra thừa số nguyên tố rồi tìm tập hợp các ước số của nó
Giải:
Phân tích 84 ra thừa số nguyên tố bằng cách viết "theo cột dọc":
| 84 42 21 7 1 |
2 2 3 7 |
Do đó: 84 = 2 . 2 . 3 . 7 = 22 . 3 . 7
+ Khi đó ta có phân tích
84 = 1 . 84 = 2. 42 = 3 . 28 = 4 . 21 = 6 . 14 = 7 . 12
Do đó các ước của 84 là: 1; 2; 3; 4; 6; 7; 12; 14; 21; 28; 42; 84.
Giả sử A là tập hợp các ước của 84.
Vậy A = {1; 2; 3; 4; 6; 7; 12; 14; 21; 28; 42; 84}.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
 Giải SGK Toán 6 chương 1, bài 12: Ước chung và ước chung lớn nhất - Sách Cánh diều
Giải SGK Toán 6 chương 1, bài 12: Ước chung và ước chung lớn nhất - Sách Cánh diều