Giải Toán 8 sách Kết nối Tri Thức, bài 13: Hình chữ nhật
Giải Toán 8 sách Kết nối Tri Thức, bài 13: Hình chữ nhật - Trang 64, 65, 66.
1. Hình chữ nhật
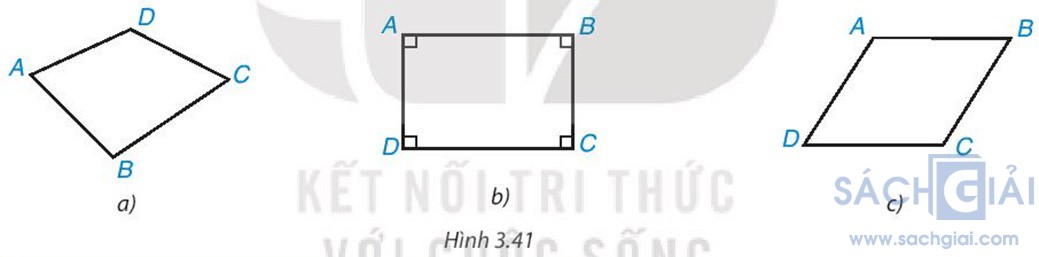
Hoạt động 1 trang 64: Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
Giải:
Hình b) là hình chữ nhật bởi có 4 góc vuông
Hoạt động 2 trang 64: Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?
Giải:
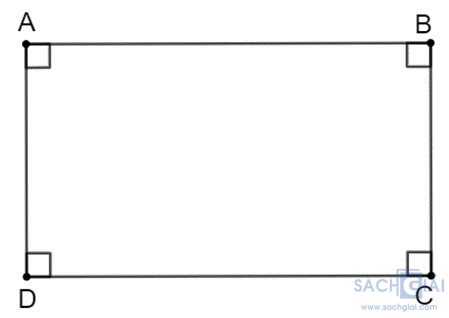
Ta đặt hình chữ nhật ABCD như hình vẽ.
Vì ABCD là hình chữ nhật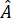 =
= 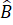 =
= 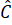 =
= 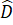 = 90o
= 90o
Ta có: AB ⊥ AD; AB ⊥ BC suy ra AD // BC.
AB ⊥ AD; CD ⊥ AD suy ra AB // CD.
Vì ABCD là hình chữ nhật nên AD // BC; AB // CD
Suy ra ABCD cũng là hình bình hành.
Vì ABCD là hình chữ nhật nên AB // CD suy ra ABCD cũng là hình thang.
Hình thang ABCD có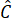 =
= 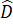 = 90o
= 90o
Do đó ABCD cũng là hình thang cân.
Luyện tập 1 trang 65: Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH\perp DC (H.3.44). Chứng minh rằng H là trung điểm của DC
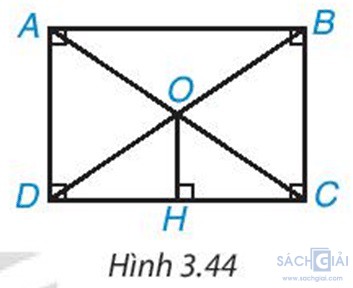
Giải:
Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra OA = OB = OC = OD.
Xét tam giác OCD cân tại O (vì OC = OD) có OH là đường cao nên OH cũng là đường trung tuyến.
Do đó CH = DH.
Vậy H là trung điểm của DC.

Giải:
Hình b) là hình chữ nhật bởi có 4 góc vuông
Hoạt động 2 trang 64: Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?
Giải:

Ta đặt hình chữ nhật ABCD như hình vẽ.
Vì ABCD là hình chữ nhật
Ta có: AB ⊥ AD; AB ⊥ BC suy ra AD // BC.
AB ⊥ AD; CD ⊥ AD suy ra AB // CD.
Vì ABCD là hình chữ nhật nên AD // BC; AB // CD
Suy ra ABCD cũng là hình bình hành.
Vì ABCD là hình chữ nhật nên AB // CD suy ra ABCD cũng là hình thang.
Hình thang ABCD có
Do đó ABCD cũng là hình thang cân.
Luyện tập 1 trang 65: Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH\perp DC (H.3.44). Chứng minh rằng H là trung điểm của DC

Giải:
Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra OA = OB = OC = OD.
Xét tam giác OCD cân tại O (vì OC = OD) có OH là đường cao nên OH cũng là đường trung tuyến.
Do đó CH = DH.
Vậy H là trung điểm của DC.
2. Dấu hiệu nhận biết
Hoạt động 3 trang 65: Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?
Giải:
Góc A vuông suy ra góc C cũng là góc vuông (do góc A và C đối nhau)
Góc A và góc D bù nhau suy ra góc D cũng là góc vuông, tương tự góc B cũng là góc vuông
Vậy tứ giác ABCD là hình chữ nhật
Luyện tập 2 trang 66: Cho tứ giác ABCD có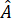 = 90o, hai đường chéo cắt nhau tạ trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?
= 90o, hai đường chéo cắt nhau tạ trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?
Giải:
Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường suy ra ABCD là hình bình hành.
Xét hình bình hành ABCD có: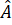 = 90o suy ra ABCD là hình chữ nhật
= 90o suy ra ABCD là hình chữ nhật
Vận dụng trang 66: Hãy trả lời các câu hỏi trong tình huống mở đầu.
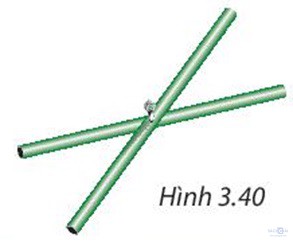
Hai thanh tre thẳng dài bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
Giải:
Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.
Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.
Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.
Giải:
Góc A vuông suy ra góc C cũng là góc vuông (do góc A và C đối nhau)
Góc A và góc D bù nhau suy ra góc D cũng là góc vuông, tương tự góc B cũng là góc vuông
Vậy tứ giác ABCD là hình chữ nhật
Luyện tập 2 trang 66: Cho tứ giác ABCD có
Giải:
Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường suy ra ABCD là hình bình hành.
Xét hình bình hành ABCD có:
Vận dụng trang 66: Hãy trả lời các câu hỏi trong tình huống mở đầu.
Hai thanh tre thẳng dài bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?

Giải:
Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.
Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.
Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.
3. Giải bài tập trang 66
Bài 3.25: Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật không. Hãy giải thích kết quả.
Giải:
Dùng ê ke để kiểm tra các góc của hình tứ giác có phải góc vuông hay không, nếu tất cả các góc đều là góc vuông thì tứ giác đó là hình chữ nhật (theo định nghĩa hình chữ nhật là tứ giác có 4 góc vuông)
Bài 3.26: Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật không. Hãy giải thích kết quả
Giải:
Ta kiểm tra xem các cặp đối của tứ giác:
• Nếu các cặp cạnh đối không bằng nhau thì tứ giác đó không là hình bình hành nên cũng không là hình chữ nhật.
• Nếu các cặp cạnh đối bằng nhau thì tứ giác đó là hình bình hành.
Sau đó ta kiểm tra xem hai đường chéo của tứ giác (là hình bình hành) đó.
• Nếu hai đường chéo của hình bình hành đó bằng nhau thì tứ giác đó là hình chữ nhật.
• Nếu hai đường chéo của hình bình hành đó không bằng nhau thì tứ giác đó không là hình chữ nhật.
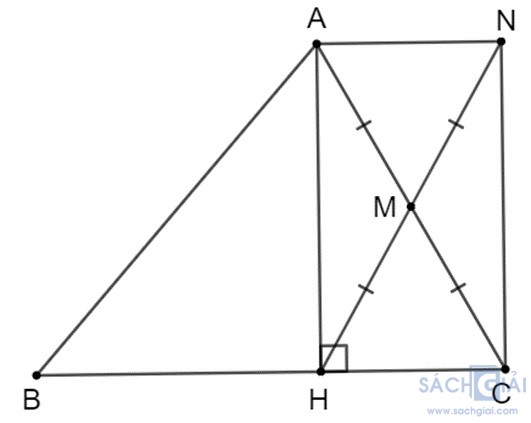
Bài 3.27: Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.
Giải:
Theo đề bài, M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN.
Nên tứ giác ANCH có hai đường chéo AC và HN cắt nhau tại trung điểm M của mỗi đường.
Suy ra tứ giác ANCH là hình bình hành.
Hình bình hành ANCH có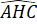 = 90o nên tứ giác ANCH là hình chữ nhật.
= 90o nên tứ giác ANCH là hình chữ nhật.
Bài 3.28: Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
Giải:
a) Tứ giác MNAP có tất cả các góc đều là góc vuông nên MNAP là hình chữ nhật
b) MNAP là hình chữ nhật suy ra NP = AM
Mà AM ngắn nhất khi AM ⊥ AM là đường cao của tam giác ABC
Mà tam giác ABC cân tại A nên AM cũng là đường trung tuyến, do đó M là trung điểm BC
Giải:
Dùng ê ke để kiểm tra các góc của hình tứ giác có phải góc vuông hay không, nếu tất cả các góc đều là góc vuông thì tứ giác đó là hình chữ nhật (theo định nghĩa hình chữ nhật là tứ giác có 4 góc vuông)
Bài 3.26: Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật không. Hãy giải thích kết quả
Giải:
Ta kiểm tra xem các cặp đối của tứ giác:
• Nếu các cặp cạnh đối không bằng nhau thì tứ giác đó không là hình bình hành nên cũng không là hình chữ nhật.
• Nếu các cặp cạnh đối bằng nhau thì tứ giác đó là hình bình hành.
Sau đó ta kiểm tra xem hai đường chéo của tứ giác (là hình bình hành) đó.
• Nếu hai đường chéo của hình bình hành đó bằng nhau thì tứ giác đó là hình chữ nhật.
• Nếu hai đường chéo của hình bình hành đó không bằng nhau thì tứ giác đó không là hình chữ nhật.
Bài 3.27: Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.

Giải:
Theo đề bài, M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN.
Nên tứ giác ANCH có hai đường chéo AC và HN cắt nhau tại trung điểm M của mỗi đường.
Suy ra tứ giác ANCH là hình bình hành.
Hình bình hành ANCH có
Bài 3.28: Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
Giải:
a) Tứ giác MNAP có tất cả các góc đều là góc vuông nên MNAP là hình chữ nhật
b) MNAP là hình chữ nhật suy ra NP = AM
Mà AM ngắn nhất khi AM ⊥ AM là đường cao của tam giác ABC
Mà tam giác ABC cân tại A nên AM cũng là đường trung tuyến, do đó M là trung điểm BC
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025