Giải SGK Toán 7 sách Kết nối tri thức, bài 7: Tập hợp các số thực
Giải SGK Toán 7 sách Kết nối tri thức, bài 7:Tập hợp các số thực - Trang 33,...
1. Khái niệm số thực và trục số thực
Luyện tập 1 - Trang 33: Cách viết nào sau đây là đúng:
a) Cách viết nào sau đây đúng: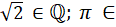 II; 15
II; 15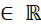
b) Viết số đối của các số: 5,08(299); -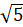
Giải:

Câu hỏi trang 34: Điểm nào trong Hình 2.4 biểu diễn số -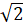
Em có nhận xét gì về điểm biểu diễn của hai số đối nhau?

Giải:
Điểm N trong Hình 2.4 biểu diễn số -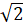
Nhận xét: Điểm biểu diễn của hai số đối nhau cách đều điểm O.
Luyện tập 2 - Trang 34: Cho biết nếu một tam giác vuông có hai cạnh góc vuông bằng 1 và 3 thì cạnh huyền của tam giác bằng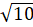
Em hãy vẽ điểm biểu diễn số -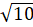 trên trục số.
trên trục số.
Giải:
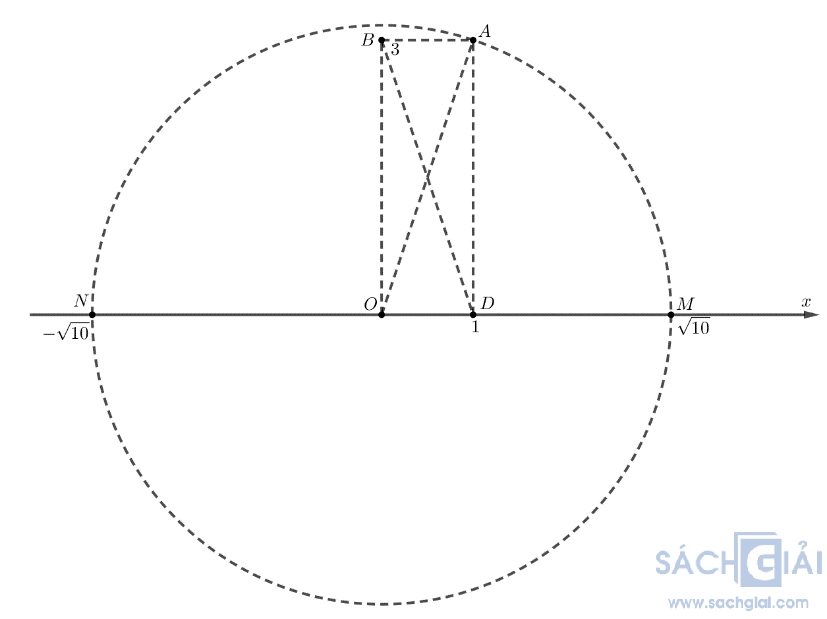
Vẽ hình chữ nhật OBAD có 2 cạnh bằng 3 và 1. Khi đó OA =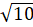
Đường tròn tâm O, bán kính OA cắt tia Ox tại điểm M.
Khi đó OM =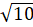
Ở bên trái điểm O lấy điểm N sao cho OM = ON.
Khi đó ON =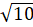
Do đó N là điểm biểu diễn số -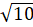
a) Cách viết nào sau đây đúng:
b) Viết số đối của các số: 5,08(299); -
Giải:

Câu hỏi trang 34: Điểm nào trong Hình 2.4 biểu diễn số -
Em có nhận xét gì về điểm biểu diễn của hai số đối nhau?

Giải:
Điểm N trong Hình 2.4 biểu diễn số -
Nhận xét: Điểm biểu diễn của hai số đối nhau cách đều điểm O.
Luyện tập 2 - Trang 34: Cho biết nếu một tam giác vuông có hai cạnh góc vuông bằng 1 và 3 thì cạnh huyền của tam giác bằng
Em hãy vẽ điểm biểu diễn số -
Giải:

Vẽ hình chữ nhật OBAD có 2 cạnh bằng 3 và 1. Khi đó OA =
Đường tròn tâm O, bán kính OA cắt tia Ox tại điểm M.
Khi đó OM =
Ở bên trái điểm O lấy điểm N sao cho OM = ON.
Khi đó ON =
Do đó N là điểm biểu diễn số -
2. Thứ tự trong tập hợp các số thực
Luyện tập 3 - Trang 35 So sánh:
a) 1,313233… và 1,(32);
b)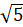 và 2,36 (có thể dùng máy tính cầm tay để tính
và 2,36 (có thể dùng máy tính cầm tay để tính 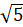 )
)
Giải:
a) 1,(32) = 1,323232… nên 1,313233… < 1,323232… hay 1,313233… < 1,(32).
Vậy 1,313233… < 1,(32).
b) Sử dụng máy tính cầm tay tính
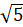 ta được kết quả là 2,236067977.
ta được kết quả là 2,236067977.
Làm tròn kết quả với độ chính xác 0,005 được
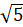 ≈ 2,24
≈ 2,24
Do 2,24 < 2,36 nên
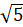 < 2,36
< 2,36
Vậy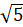 < 2,36
< 2,36
a) 1,313233… và 1,(32);
b)
Giải:
a) 1,(32) = 1,323232… nên 1,313233… < 1,323232… hay 1,313233… < 1,(32).
Vậy 1,313233… < 1,(32).
b) Sử dụng máy tính cầm tay tính
Làm tròn kết quả với độ chính xác 0,005 được
Do 2,24 < 2,36 nên
Vậy
3. Giá trị tuyệt đối của một số thực
Hoạt động 1 - Trang 35: Biểu diễn các số 3 và –2 trên trục số rồi cho biết mỗi điểm ấy cách gốc O bao nhiêu đơn vị.
Giải:
Điểm A và B lần lượt là hai điểm biểu diễn các số 3 và –2 trên trục số.

Điểm B cách gốc O một khoảng bằng 2 đơn vị, điểm A cách gốc O một khoảng bằng 3 đơn vị.
Hoạt động 2 - Trang 35: Không vẽ hình, hãy cho biết khoảng cách của mỗi điểm sau đến gốc O: –4; –1; 0; 1; 4.
Giải:
Khoảng cách từ –4 đến gốc O là 4 đơn vị.
Khoảng cách từ –1 đến gốc O là 1 đơn vị.
Khoảng cách từ 0 đến gốc O là 0 đơn vị.
Khoảng cách từ 1 đến gốc O là 1 đơn vị.
Khoảng cách từ 4 đến gốc O là 4 đơn vị.
Câu hỏi trang 35: Từ hoạt động 1 và hoạt động 2, hãy tìm giá trị tuyệt đối của các số: 3; –2; 0; 4 và –4.
Giải:
Giá trị tuyệt đối của 3 là |3| = 3
Giá trị tuyệt đối của –2 là |−2| = 2
Giá trị tuyệt đối của 0 là |0| = 0.
Giá trị tuyệt đối của 4 là |4| = 4
Giá trị tuyệt đối của –4 là |−4| = 4
Câu hỏi trang 36: Minh viết |−2,5| = -2,5 là đúng hay sai?
Giải:
Do –2,5 < 0 nên |−2,5| = - (2,5) = 2,5
Vậy Minh viết sai.
Luyện tập 4 - Trang 36: Tính: a)
a) |-2,3|;
b)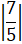
c) |-11|;
d)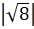
Giải:
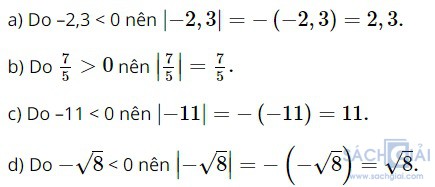
Thử thách nhỏ trang 36: Liệt kê các phần tử của tập hợp
A = {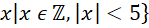
Giải:
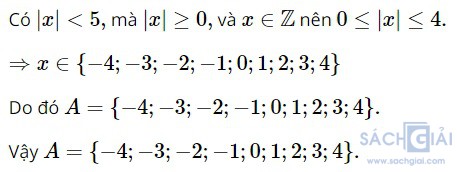
Giải:
Điểm A và B lần lượt là hai điểm biểu diễn các số 3 và –2 trên trục số.

Điểm B cách gốc O một khoảng bằng 2 đơn vị, điểm A cách gốc O một khoảng bằng 3 đơn vị.
Hoạt động 2 - Trang 35: Không vẽ hình, hãy cho biết khoảng cách của mỗi điểm sau đến gốc O: –4; –1; 0; 1; 4.
Giải:
Khoảng cách từ –4 đến gốc O là 4 đơn vị.
Khoảng cách từ –1 đến gốc O là 1 đơn vị.
Khoảng cách từ 0 đến gốc O là 0 đơn vị.
Khoảng cách từ 1 đến gốc O là 1 đơn vị.
Khoảng cách từ 4 đến gốc O là 4 đơn vị.
Câu hỏi trang 35: Từ hoạt động 1 và hoạt động 2, hãy tìm giá trị tuyệt đối của các số: 3; –2; 0; 4 và –4.
Giải:
Giá trị tuyệt đối của 3 là |3| = 3
Giá trị tuyệt đối của –2 là |−2| = 2
Giá trị tuyệt đối của 0 là |0| = 0.
Giá trị tuyệt đối của 4 là |4| = 4
Giá trị tuyệt đối của –4 là |−4| = 4
Câu hỏi trang 36: Minh viết |−2,5| = -2,5 là đúng hay sai?
Giải:
Do –2,5 < 0 nên |−2,5| = - (2,5) = 2,5
Vậy Minh viết sai.
Luyện tập 4 - Trang 36: Tính: a)
a) |-2,3|;
b)
c) |-11|;
d)
Giải:
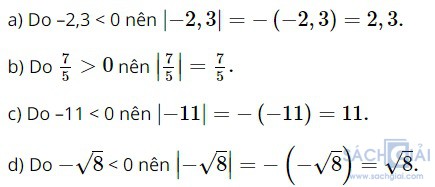
Thử thách nhỏ trang 36: Liệt kê các phần tử của tập hợp
A = {
Giải:
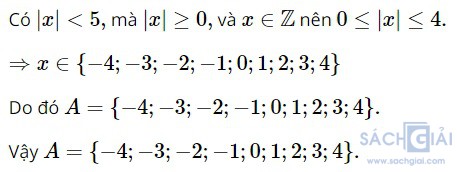
* Bài tập trang 36
Bài 2.13 - Trang 36: Xét tập hợp 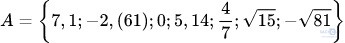 . Bằng cách liệt kê phần tử, hãy viết tập hợp B gồm các số hữu tỉ thuộc tập A và tập hợp C gồm các số vô tỉ.
. Bằng cách liệt kê phần tử, hãy viết tập hợp B gồm các số hữu tỉ thuộc tập A và tập hợp C gồm các số vô tỉ.
Giải:

Bài 2.14 - Trang 36: Gọi A’ là tập hợp các số đối của các số thuộc tập A trong bài tập 2.13. Liệt kê các phần tử của A’
Giải:
Số đối của số 7,1 là -7,1
Số đối của số -2,(61) là 2,(61)
Số đối của số 0 là 0
Số đối của số 5,14 là -5,14
Số đối của số \frac{4}{7} là - \frac{4}{7}
Số đối của số \sqrt {15} là - \sqrt {15}
Số đối của số - \sqrt {81} = \sqrt {81}
Bài 2.15 - Trang 36: Mũi tên màu xanh trong mỗi hình sau chỉ số thực nào?
Giải:
a.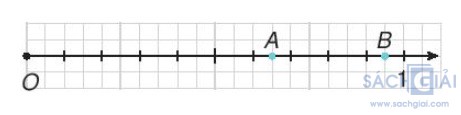
Quan sát hình ta thấy đoạn thẳng đơn vị (từ gốc O đến số 1) được chia thành 10 đoạn bằng nhau, mỗi đoạn đó lại được chia thành 2 đoạn nhỏ bằng nhau, như vậy đoạn thẳng đơn vị được chia thành 20 đoạn đơn vị mới có độ dài bằng nhau và bằng 1/20 độ dài đoạn thẳng đơn vị cũ.
Điểm A nằm ở bên phải điểm O (nằm sau điểm O) và cách O một khoảng bằng 13 đoạn đơn vị mới nên điểm A biểu diễn số 13/20
Điểm B nằm ở bên phải điểm O (nằm sau điểm O) và cách O một khoảng bằng 19 đoạn đơn vị mới nên điểm B biểu diễn số 19/20
b)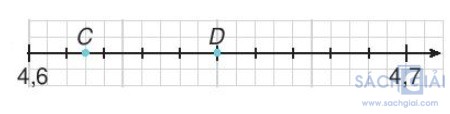
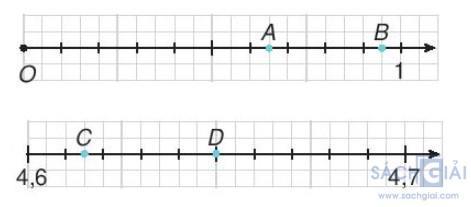
Ta có: 4,7 – 4,6 = 0,1.
Chia đoạn thẳng 0,1 thành 20 phần bằng nhau, nên mỗi đoạn bằng 0,1/20
Điểm C nằm ở bên phải điểm 4,6 và cách điểm 4,6 một khoảng bằng 3 đoạn 0,005 nên điểm đó biểu diễn số 4,6 + 3.0,005 = 4,615.
Điểm D nằm ở bên phải điểm 4,6 và cách điểm 4,6 một khoảng bằng 10 đoạn 0,005 nên điểm đó biểu diễn số 4,6 + 10.0,005 = 4,65.
Bài 2.16 - Trang 36: Tính:
a. |-3,5|
b.
c. |0|
d. |2,0(3)|
Giải:
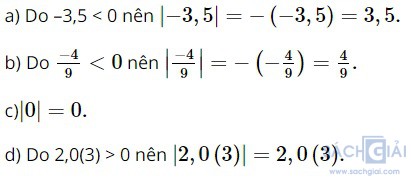
Bài 2.17 - Trang 36: Xác định dấu và giá trị tuyệt đối của mỗi số sau:
a) a = 1,25;
b) b = - 4,1;
c) c = - 1,414213562....
Giải:
a) a = 1,25 có dấu dương, |a| = |1,25| = 1,25
b) b = - 4,1 có dấu âm, |b| = | - 4,1| = 4,1
c) c = - 1,414213562.... có dấu âm,|c| = | - 1,414213562....| = 1,414213562....
Bài 2.18 - Trang 36: Tìm tất cả các số thực x thỏa mãn điều kiện |x| = 2,5
Giải:
Nếu x ≥ 0 thì |x| = x, mà |x| = 2,5 nên x = 2,5.
Nếu x < 0 thì |x|= −x, mà |x| = 2,5 nên –x = 2,5 do đó x = –2,5.
Vậy x = –2,5 hoặc x = 2,5.
Giải:

Bài 2.14 - Trang 36: Gọi A’ là tập hợp các số đối của các số thuộc tập A trong bài tập 2.13. Liệt kê các phần tử của A’
Giải:
Số đối của số 7,1 là -7,1
Số đối của số -2,(61) là 2,(61)
Số đối của số 0 là 0
Số đối của số 5,14 là -5,14
Số đối của số \frac{4}{7} là - \frac{4}{7}
Số đối của số \sqrt {15} là - \sqrt {15}
Số đối của số - \sqrt {81} = \sqrt {81}
Bài 2.15 - Trang 36: Mũi tên màu xanh trong mỗi hình sau chỉ số thực nào?

Giải:
a.

Quan sát hình ta thấy đoạn thẳng đơn vị (từ gốc O đến số 1) được chia thành 10 đoạn bằng nhau, mỗi đoạn đó lại được chia thành 2 đoạn nhỏ bằng nhau, như vậy đoạn thẳng đơn vị được chia thành 20 đoạn đơn vị mới có độ dài bằng nhau và bằng 1/20 độ dài đoạn thẳng đơn vị cũ.
Điểm A nằm ở bên phải điểm O (nằm sau điểm O) và cách O một khoảng bằng 13 đoạn đơn vị mới nên điểm A biểu diễn số 13/20
Điểm B nằm ở bên phải điểm O (nằm sau điểm O) và cách O một khoảng bằng 19 đoạn đơn vị mới nên điểm B biểu diễn số 19/20
b)

Ta có: 4,7 – 4,6 = 0,1.
Chia đoạn thẳng 0,1 thành 20 phần bằng nhau, nên mỗi đoạn bằng 0,1/20
Điểm C nằm ở bên phải điểm 4,6 và cách điểm 4,6 một khoảng bằng 3 đoạn 0,005 nên điểm đó biểu diễn số 4,6 + 3.0,005 = 4,615.
Điểm D nằm ở bên phải điểm 4,6 và cách điểm 4,6 một khoảng bằng 10 đoạn 0,005 nên điểm đó biểu diễn số 4,6 + 10.0,005 = 4,65.
Bài 2.16 - Trang 36: Tính:
a. |-3,5|
b.
c. |0|
d. |2,0(3)|
Giải:
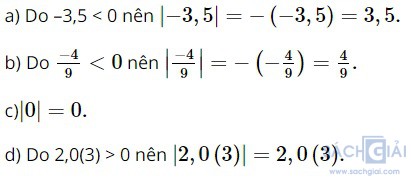
Bài 2.17 - Trang 36: Xác định dấu và giá trị tuyệt đối của mỗi số sau:
a) a = 1,25;
b) b = - 4,1;
c) c = - 1,414213562....
Giải:
a) a = 1,25 có dấu dương, |a| = |1,25| = 1,25
b) b = - 4,1 có dấu âm, |b| = | - 4,1| = 4,1
c) c = - 1,414213562.... có dấu âm,|c| = | - 1,414213562....| = 1,414213562....
Bài 2.18 - Trang 36: Tìm tất cả các số thực x thỏa mãn điều kiện |x| = 2,5
Giải:
Nếu x ≥ 0 thì |x| = x, mà |x| = 2,5 nên x = 2,5.
Nếu x < 0 thì |x|= −x, mà |x| = 2,5 nên –x = 2,5 do đó x = –2,5.
Vậy x = –2,5 hoặc x = 2,5.
Ý kiến bạn đọc
Theo dòng sự kiện
Những tin mới hơn
Những tin cũ hơn
DANH MỤC
Bài học mới
-
 Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
Hãy viết bài văn nghị luận bàn về lối sống phông bạt của giới trẻ hiện nay
-
 Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
Đề kiểm tra cuối học kì 1, môn: Tin học 6 Kết nối tri thức
-
 Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
Đề kiểm tra giữa học kì 1, môn: Giáo dục công dân 6 Kết nối tri thức
-
 Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Ngữ Văn, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Toán, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
-
 Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
Đề thi tham khảo môn Tiếng Anh, kỳ thi đánh giá năng lực xét tuyển đại học hệ chính quy năm 2025
 Giải SGK Toán 7 sách Kết nối tri thức, bài 6: Số vô tỉ. Căn bậc hai số học
Giải SGK Toán 7 sách Kết nối tri thức, bài 6: Số vô tỉ. Căn bậc hai số học